
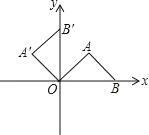
【题目】在直角坐标系中,等腰直角三角形AOB在如图所示的位置,点B的横坐标为2,将△AOB绕点O按逆时针方向旋转90°,得到△A′OB′,则点A′的坐标为( )
A. (1,1) B. (![]() ,
,![]() )
)
C. (﹣1,1) D. (﹣![]() ,
,![]() )
)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
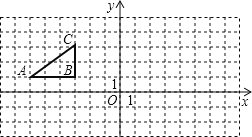
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
(1)将原来的Rt△ABC绕点O顺时针旋转90°得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形.
(2)求线段BC扫过的面积.
(3)求点A旋转到A1路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题.我们知道,![]() ,
,![]() ,…,如果两个含有二次根式的非零代数式相乘,它们的积不含二次根式,就说这两个非零代数式互为有理化因式.如
,…,如果两个含有二次根式的非零代数式相乘,它们的积不含二次根式,就说这两个非零代数式互为有理化因式.如![]() 与
与![]() 互为有理化因式,
互为有理化因式,![]() 和
和![]() 互为有理化因式.根据互为有理化因式的积是有理数,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化.例如:
互为有理化因式.根据互为有理化因式的积是有理数,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化.例如:![]() .请解答下列问题:
.请解答下列问题:
(1)![]() 分母有理化的结果是 ;
分母有理化的结果是 ;![]() 分母有理化的结果是 ;
分母有理化的结果是 ;
(2)计算:![]() ;
;
(3)若实数![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
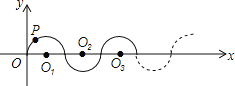
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是( )
个单位长度,则第2019秒时,点P的坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
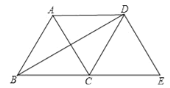
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是________________(填写正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
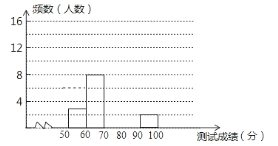
【题目】为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 3 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 13 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 2 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(4)第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导,则第4组的小宇与小强能同时抽到的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
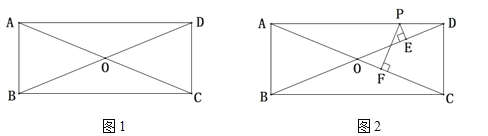
【题目】如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com