
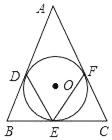
【题目】如图,△ABC的三边分别切⊙O于D,E,F.
(1)若∠A=40°,求∠DEF的度数;
(2)AB=AC=13,BC=10,求⊙O的半径.
科目:初中数学 来源: 题型:
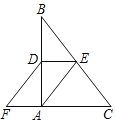
【题目】如图,在Rt△ABC中∠BAC=90°,D,E分别是AB,BC的中点,F在CA的延长线上∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法.
问题提出:求边长分别为、![]() 、
、![]() 、
、![]() 的三角形面积.
的三角形面积.
问题解决:
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
![]() 、
、![]() 、
、![]() 的格点三角形
的格点三角形![]() (如图),
(如图),![]() 是角边为1和2的直角三角形斜边,
是角边为1和2的直角三角形斜边,![]() 是直角边分别为1和3的直角三角形的斜边,
是直角边分别为1和3的直角三角形的斜边,![]() 是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求
是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求![]() 的高,而借用网格就能计算它的面积.
的高,而借用网格就能计算它的面积.
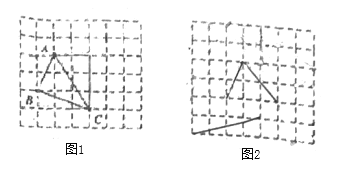
(1)请直接写出图①中![]() 的面积为____________.
的面积为____________.
(2)类比迁移:求边长分别为![]() 、
、![]() 、
、![]() 的三角形面积(请利用图②的正方形网格画出相应的
的三角形面积(请利用图②的正方形网格画出相应的![]() ,并求出它的面积)
,并求出它的面积)
(3)思维拓展:求边长分别为![]() ,的三角形的面积
,的三角形的面积
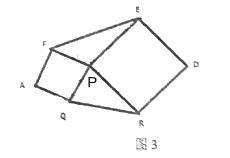
(4)如图(3),已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,正方形
,正方形![]() ,连接
,连接![]() ,若
,若![]() ,则六边形
,则六边形 ![]() 的面积是_________.
的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
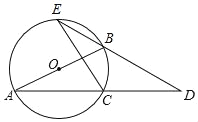
【题目】如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E.
(1)求证:CD=CE;
(2)连结AE,若∠D=25°,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
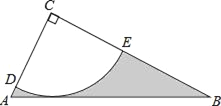
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,BC=2AC,半径为2的⊙C,分别交AC、BC于点D、E,得到
,BC=2AC,半径为2的⊙C,分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
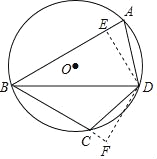
【题目】如图,四边形ABCD是⊙O的内接四边形,BD是∠ABC的角平分线,过点D分别作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:△AED≌△CFD;
(2)若AB=10,BC=8,∠ABC=60°,求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
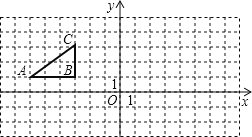
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
(1)将原来的Rt△ABC绕点O顺时针旋转90°得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形.
(2)求线段BC扫过的面积.
(3)求点A旋转到A1路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
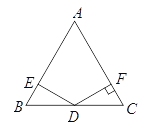
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图,若DF⊥AC,垂足为F,证明:DE=DF
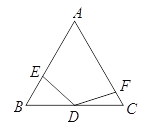
(2)如图,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.DE=DF仍然成立吗?说明理由。
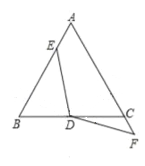
(3)将∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,DE=DF仍然成立吗? 直接说出结论,不必说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题.我们知道,![]() ,
,![]() ,…,如果两个含有二次根式的非零代数式相乘,它们的积不含二次根式,就说这两个非零代数式互为有理化因式.如
,…,如果两个含有二次根式的非零代数式相乘,它们的积不含二次根式,就说这两个非零代数式互为有理化因式.如![]() 与
与![]() 互为有理化因式,
互为有理化因式,![]() 和
和![]() 互为有理化因式.根据互为有理化因式的积是有理数,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化.例如:
互为有理化因式.根据互为有理化因式的积是有理数,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化.例如:![]() .请解答下列问题:
.请解答下列问题:
(1)![]() 分母有理化的结果是 ;
分母有理化的结果是 ;![]() 分母有理化的结果是 ;
分母有理化的结果是 ;
(2)计算:![]() ;
;
(3)若实数![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com