
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图,若DF⊥AC,垂足为F,证明:DE=DF
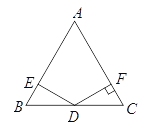
(2)如图,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.DE=DF仍然成立吗?说明理由。
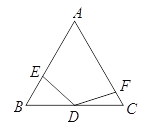
(3)将∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,DE=DF仍然成立吗? 直接说出结论,不必说明理由。
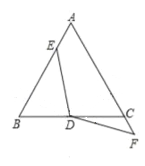
【答案】(1)证明见解析(2)成立 (3)成立
【解析】
(1)证明△ABC是等边三角形,得∠B=∠C,BD=CD,进而证明△BED≌△CFD(ASA),即可证明DE=DF.
(2)取AC中点G,连接DG,证明△EDG≌△FDC(ASA),即可证明结论仍成立.
(3)过点D作DN⊥AC于N,DM⊥AB于M,得∠NDF=∠MDE,证明△DME≌△DNF(ASA)即可证明结论仍成立.
解:(1)∵AB=AC,∠A=60°,
∴△ABC是等边三角形,即∠B=∠C=60°,
∵D是BC的中点,
∴BD=CD,
∵∠EDF=120°,DF⊥AC,
∴∠FDC=30°,
∴∠EDB=30°,
∴△BED≌△CFD(ASA),
∴DE=DF.
(2)取AC中点G,连接DG,如下图,
∵D为BC的中点,
∴DG=![]() AC=BD=CD,
AC=BD=CD,
∴△BDG是等边三角形,
∴∠GDE+∠EDB=60°,
∵∠EDF=120°,
∴∠FDC+∠EDB=60°,
∴∠EDG=∠FDC,
∴△EDG≌△FDC(ASA),
∴DE=DF.
∴结论仍然成立.
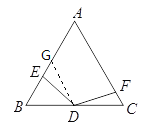
(3)如下图,过点D作DN⊥AC于N,DM⊥AB于M,
∴∠DME=∠DNF=90°,
由(1)可知∠B=∠C=60°,
∴∠NDC=∠BDM=30°,DM=DN,
∴∠MDN=120°,即∠NDF=∠MDE,
∴△DME≌△DNF(ASA),
∴DE=DF,
∴仍然成立.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
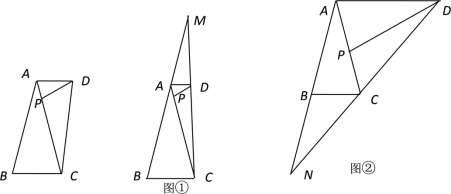
【题目】如图,在△ABC中,AB=AC=10,BC=5,点P是边AC上的一个动点,∠APD=∠ABC,AD∥BC,连接CD.
(1)求证AD=2AP;
(2)如图①,若BA与CD的延长线交于点M,AP=1,求AM的长;
(3)如图②,若AB与DC的延长线交于点N,当△CDP与△BCN相似时,求证点P是AC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
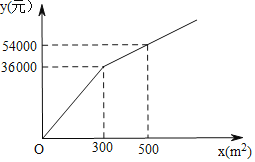
【题目】如图,为了美化环境,建设魅力呼和浩特,呼和浩特市准备在一个广场上种植甲、乙两种花卉经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示乙种花卉的种植费用为每平方米100元
之间的函数关系如图所示乙种花卉的种植费用为每平方米100元
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
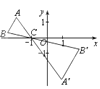
A. -![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com