
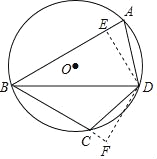
【题目】如图,四边形ABCD是⊙O的内接四边形,BD是∠ABC的角平分线,过点D分别作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:△AED≌△CFD;
(2)若AB=10,BC=8,∠ABC=60°,求BD的长度.
【答案】(1)见解析;(2)6![]() .
.
【解析】
(1)由角平分线性质定理可得DE=DF,由圆内接四边形性质可得∠A+∠BCD=180°,然后代换可得∠A=∠DCF,又∠DEA=∠F=90°, 所以△AED≌△CFD;(2)由三角形全等可得AE=CF,BE=BF,设AE=CF=x,可得x=1;在Rt△BFD,根据30°所对的直角边是斜边的一半,则BD=2DF,利用勾股定理解得BD=6![]() .
.
(1)∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,
又∵∠DCF+∠BCD=180°,∴∠A=∠DCF
∵BD是∠ABC的角平分线,又∵DE⊥AB,DF⊥BC,
∴DE=DF,
∠DEA=∠F=90°,
∴△AED≌△CFD.
(2)∵△AED≌△CFD,∴AE=CF,BE=BF,
设AE=CF=x,则BE=10-x,BF=8+x,
即10-x=8+x,解得x=1,
在Rt△BFD,∠DBC=30°,设DF=y,则BD=2y,
∵BF2+DF2=BD2,
∴y2+92=(2y)2,y=3![]() ,
,
BD=6![]() .
.


科目:初中数学 来源: 题型:
【题目】某文具商店的某种毛笔每支售价25元,书法练习本每本售价5元,该商店为促销正在进行优惠活动:
活动1:买一支毛笔送一本书法练习本;
活动2:按购买金额的九折付款.
某学校准备为书法兴趣小组购买这种毛笔20支,书法练习本x(x≥20)本.
(1)写出两种优惠活动实际付款金额y1(元),y2(元)与x(本)之间的函数关系式;
(2)请问:该校选择哪种优惠活动更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
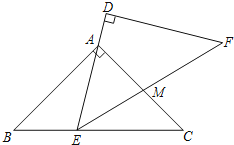
【题目】△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=![]() .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .作DE⊥AC于点E,作AF⊥BD于点F.
.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点![]() 为圆心作圆,
为圆心作圆, ![]() 、
、![]() 、
、![]() 、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求
、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求![]() 的半径
的半径 ![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工两名,采取笔试与面试相结合的方式进行,两项成绩原始分满分均为100分,前六名选手的得分如下:
序号项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩(分) | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩(分) | 90 | 83 | 82 | 90 | 80 | 85 |
(1)这6名选手笔试成绩的中位数是________分,众数是________分.
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)在(2)的情况下________,(填序号)选手会被录取.
查看答案和解析>>
科目:初中数学 来源: 题型:
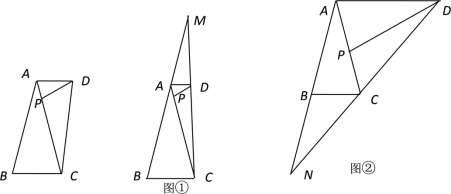
【题目】如图,在△ABC中,AB=AC=10,BC=5,点P是边AC上的一个动点,∠APD=∠ABC,AD∥BC,连接CD.
(1)求证AD=2AP;
(2)如图①,若BA与CD的延长线交于点M,AP=1,求AM的长;
(3)如图②,若AB与DC的延长线交于点N,当△CDP与△BCN相似时,求证点P是AC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟) | 0 | 10 | … | 25 |
水池的容积V(公升) | 100 | 300 | … | 600 |
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com