
����Ŀ����ͼ����֪������y=ax2+bx+c��x���һ������A������Ϊ����1��0�����Գ���Ϊֱ��x=��2��
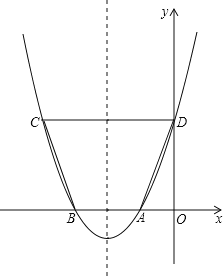
��1������������x�����һ������B�����ꣻ
��2����D����������y��Ľ��㣬��C���������ϵ���һ�㣮��֪��ABΪһ�ױߵ�����ABCD�����Ϊ9����������ߵĽ���ʽ����ָ������E�����ꣻ
��3����P�ǣ�2���������߶Գ�����һ���㣬����1����λ/����ٶȴӴ������ߵĶ���E�����˶������P�˶���ʱ��Ϊt�룮
����tΪ�� ����ʱ����PAD���ܳ���С����tΪ�� ����ʱ����PAD����ADΪ���ĵ��������Σ�������������ţ�
����P���˶������У��Ƿ����һ��P��ʹ��PAD����ADΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1���������ߵ���Գ��Լ�A����1��0�����ɵ�B����3��0����
��2���������ߵĶԳ��ύCD�ڵ�M����AB�ڵ�N��

�������֪AB��CD���������ߵ���Գ��Կɵ�CD=2DM��
��MN��y�ᣬAB��CD�����ı���ODMN�Ǿ��Ρ�
��DM=ON=2����CD=2��2=4��
��A����1��0����B����3��0������AB=2��
������ABCD�����=![]() ��AB+CD��OD=9��
��AB+CD��OD=9��
��OD=3����c=3��
��A����1��0����B����3��0������y=ax2+bx+3��
![]() �����
�����![]() ��
��
��y=x2+4x+3��
��y=x2+4x+3��Ϊ����ʽΪy=��x+2��2��1����E����2����1������
��3����2�� 4��![]() ��
��![]() ��
��
�����ڡ�
�ߡ�APD=90�㣬��PMD=��PNA=90�㣬���PDM+��APN=90�㣬��DPM+��PDM=90�㡣
���PDM=��APN��
�ߡ�PMD=��ANP�����APN�ס�PDM��
��![]() ����
����![]() ��
��
��PN2��3PN+2=0�����PN=1��PN=2��
��P����2��1����2��2����
��������
������1�����������ߵ���Գ��Կɵ���������x�����һ������B��������
��2���ȸ�������ABCD�����Ϊ9������c��ֵ�������ô���ϵ�������������ߵĽ���ʽ��ת��Ϊ����ʽ����E��������
��3����������ԳƩ����·��������ɵ���PAD���ܳ���Сʱt��ֵ�����ݵ��������ε����ʿɷ�������������PAD����ADΪ���ĵ���������ʱt��ֵ��
����֤����APN�ס�PDM���������������ε��������PN��ֵ���Ӷ��õ���P��������


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
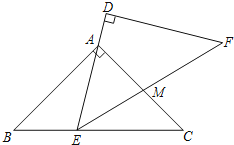
����Ŀ����ABC���DEF������ȫ�ȵĵ���ֱ�������Σ���BAC=��D=90����AB=AC=![]() ���ֽ���DEF���ABC����ͼ��ʾ�ķ�ʽ������һ��ʹ��ABC���ֲ�������DEF�˶����������E�ڱ�BC���˶�������B��C�غϣ�����DEʼ�վ�����A��EF��AC���ڵ�M���ڡ�DEF�˶������У�����AEM�ܹ��ɵ��������Σ���BE�ij�Ϊ______��
���ֽ���DEF���ABC����ͼ��ʾ�ķ�ʽ������һ��ʹ��ABC���ֲ�������DEF�˶����������E�ڱ�BC���˶�������B��C�غϣ�����DEʼ�վ�����A��EF��AC���ڵ�M���ڡ�DEF�˶������У�����AEM�ܹ��ɵ��������Σ���BE�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
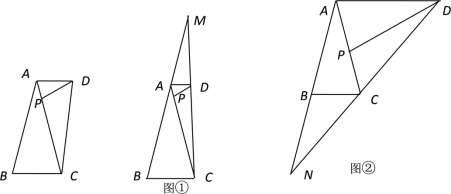
����Ŀ����ͼ������ABC�У�AB=AC=10��BC=5����P�DZ�AC�ϵ�һ�����㣬��APD=��ABC��AD��BC������CD��
��1����֤AD=2AP��
��2����ͼ������BA��CD���ӳ��߽��ڵ�M��AP��1����AM�ij���
��3����ͼ������AB��DC���ӳ��߽��ڵ�N������CDP����BCN����ʱ����֤��P��AC���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() �ϵ����㣬����
�ϵ����㣬����![]() ������
������![]() ��
��![]() .
.
��1����֤![]() ��
��
��2����![]() ������
������![]() ��
��![]() ���ж��ı���
���ж��ı���![]() ����״����˵������.
����״����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
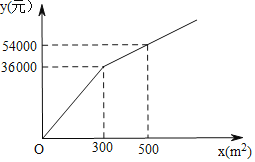
����Ŀ����ͼ��Ϊ�����������������������ͺ��أ����ͺ���������һ���㳡����ֲ�ס������ֻ��ܾ��г����飬���ֻ��ܵ���ֲ����![]() ��Ԫ������ֲ���
��Ԫ������ֲ���![]() ֮��ĺ�����ϵ��ͼ��ʾ���ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ
֮��ĺ�����ϵ��ͼ��ʾ���ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ
��1��ֱ��д����![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����![]() �������ֻ��ܵ���ֲ���������
�������ֻ��ܵ���ֲ���������![]() ���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�����й���ũ�������ʤ��80���꣬ij�̼���1200Ԫ������һ������ʤ����������������к��Ȼ����Ӧ���̼�����2800Ԫ�����˵ڶ������ּ����������������ǵ�һ����������2���������۹���5Ԫ��
��1�����̼ҹ����ĵ�һ�������������Ƕ���Ԫ��
��2������������������ͬ�ı�����ۣ����ʣ��20������۰����Ż��������������������ȫ������������640Ԫ���������������أ�����ôÿ���������ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
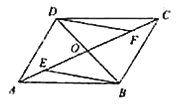
����Ŀ����֪����ͼ��E��F ��ƽ���ı��� ABCD �ĶԽ��� AC �ϵ����㣬AE=CF��

��֤����1��EB DF ��
��2��EB��DF ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һˮ�ص��ݻ�V����������ע��ˮ��ʱ��t�����ӣ�֮�俪ʼ��һ�κ�����ϵ�����м�¼�������ʱ��ע��ˮ��ʱ����ˮ���ݻ����ֶ�Ӧֵ��
ע��ˮ��ʱ��t�����ӣ� | 0 | 10 | �� | 25 |
ˮ�ص��ݻ�V�������� | 100 | 300 | �� | 600 |
��1�������ʱ��ʱV����t�ĺ�����ϵʽ������Ҫд�������Ķ�����
��2����tΪ25���ӿ�ʼ��ÿ����ע���ˮ�������仯�ˣ���tΪ27����ʱ��ˮ�ص��ݻ�Ϊ726������������������е�ÿ����ע���ˮ�������İٷ�����ͬ��������ٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
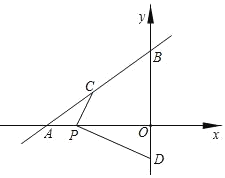
����Ŀ����ͼ��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A�͵�B����C���߶�AB�ϣ���D��y��ĸ������ϣ�C��D���㵽x��ľ����Ϊ2��
��x�ᡢy��ֱ��ڵ�A�͵�B����C���߶�AB�ϣ���D��y��ĸ������ϣ�C��D���㵽x��ľ����Ϊ2��
��1����C�������� ��������D�������� �� ����
��2����PΪ�߶�OA�ϵ�һ���㣬��PC+PD��Сʱ�����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com