
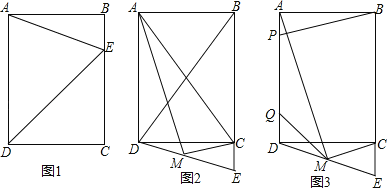
����Ŀ����֪����ͼ���ھ���ABCD�У�AB��6��BC��8��EΪֱ��BC��һ�㣮
��1����ͼ1����E���߶�BC�ϣ���DE��ADʱ����BE�ij���
��2����ͼ2����EΪBC�ӳ�������һ�㣬��BD��BE������DE��MΪED���е㣬����AM��CM����֤��AM��CM��
��3����ͼ3���ڣ�2�������£�P��QΪAD���ϵ��������㣬��PQ��5������PB��MQ��BM�����ı���PBMQ���ܳ�����Сֵ��
���𰸡���1��BE=8��2![]() ����2��֤������������3��
����2��֤������������3��![]() +5+3
+5+3![]() ��
��
��������
��1�������DE��AD��4������ù��ɶ������ɵó����ۣ�
��2�����жϳ���BMD��90�������жϳ���ADM�ա�BCM�ó���AMD����BMC�����ɵó����ۣ�
��3������BM��PQ�Ƕ�ֵ��ֻҪBP+QM��С�����öԳ�ȷ����MG'����BP+QM����Сֵ��������ù��ɶ������ɵó����ۣ�
�⣺��1����ͼ1�У����ı���ABCD�Ǿ��Σ�
���C��90����CD��AB��6��AD��BC��8��
��DE��AD��8��
��Rt��CDE��CE��![]() ��
��
��BE��BC��CE��8��2![]() ��
��
��2����ͼ2������BM��
����M��DE���е㣬
��DM��EM��
��BD��BE��
��BM��DE��
���BMD��90����
����M��Rt��CDE��б�ߵ��е㣬
��DM��CM��
���CDM����DCM��
���ADM����BCM
����ADM����BCM��
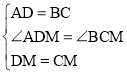 ��
��
���ADM�ա�BCM��SAS����
���AMD����BMC��
���AMC����AMB+��BMC����AMB+��AMD����BMD��90����
��AM��CM��
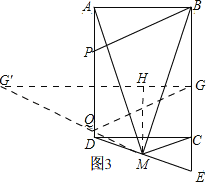
��3����ͼ3�У�����Q��QG��BP��BC��G������G����AD�ĶԳƵ�G'������QG'������G'��Q��M��ͬһ������ʱ��QM+BP��С����PQ��BM�Ƕ�ֵ��
����ʱ���ı���PBMQ�ܳ���С��
��QG��PB��PQ��BG��
���ı���BPQG��ƽ���ı��Σ�
��QG��BP��BG��PQ��5��
��CG��3����ͼ2����Rt��BCD�У�CD��6��BC��8��
��BD��10��
��BE��10��
��BG��BE��BG��5��CE��BE��BC��2��
��HM��1+3��4��HG��![]() CD��3��
CD��3��
��Rt��MHG'��HG'��6+3��9��HM��4��
��MG'��![]() ��
��
��Rt��CDE��DE��![]() ��
��
��ME��![]() ��
��
��Rt��BME��BM��![]() ��3
��3![]() ��
��
���ı���PBMQ�ܳ���СֵΪBP+PQ+MQ+BM��QG+PQ+QM+BM��MG'+PQ+PM��![]() +5+3
+5+3![]() ��
��


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��һ��
��һ��![]() ��
��![]() ����������ϣ���
����������ϣ���![]() ������Ϊ
������Ϊ![]() ��
��![]() ������
������![]() ��ԭ��
��ԭ��![]() ���������߶�
���������߶�![]() ����ÿ��2����λ���ٶ����
����ÿ��2����λ���ٶ����![]() �����˶�������
�����˶�������![]() ��ԭ��
��ԭ��![]() ��������
��������![]() �����������ÿ��1����λ���ٶ����������˶�������
�����������ÿ��1����λ���ٶ����������˶�������![]() ��
��![]() ���ƽ���߷ֱ�
���ƽ���߷ֱ�![]() ��
��![]() ���趯��
���趯��![]() ��
��![]() ͬʱ����������
ͬʱ����������![]() �����
�����![]() ʱ����
ʱ����![]() Ҳֹͣ�˶��������˶���ʱ��Ϊ
Ҳֹͣ�˶��������˶���ʱ��Ϊ![]() ��
��![]() ��
��

��1����![]() ������Ϊ_____,
������Ϊ_____,![]() ������Ϊ____��
������Ϊ____��
��2����![]() Ϊ��ֵʱ���ı���
Ϊ��ֵʱ���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
��3���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() Ϊֱ�������Σ������ڣ��������ʱ
Ϊֱ�������Σ������ڣ��������ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ֽƬ![]() �У�
��![]() ��
��![]() ����һ������ֽƬʹ��
����һ������ֽƬʹ��![]() ���
���![]() �غϣ�����
�غϣ�����![]() Ϊ�ۺۣ�����
Ϊ�ۺۣ�����![]() ��
��
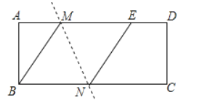
��1����֤���ı���![]() �����Σ�
������
��2����![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90����D��AB����һ�㣬��BDΪֱ���ġ�O���AC�����ڵ�E������DE���ӳ�����BC���ӳ��߽��ڵ�F��
��1����֤��BD=BF��
��2����BC=6��AD=4����sinA��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC������ΪD��AD=CD����E��AD�ϣ�DE=BD��M��N�ֱ���AB��CE���е㣮
��1����֤����ADB�ա�CDE��
��2������MDN�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�����˶�����1�δ�ԭ���˶����㣨1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�����������������˶����ɣ�������2018���˶�����P��������_____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ�������
A. ���ӻ������ڲ���棬�DZ�Ȼ�¼�
B. ������5�ε���ѧ�����У�����ͬѧ��ƽ������ͬ������ϴ��ͬѧ��ѧ�ɼ����ȶ�
C. ijͬѧ����10�������������ȵ�Ӳ�ң�3���������ϣ�����������ϵĸ�����30%
D. ��һ��ֻװ�а���ĸ�������һ�������������ǰ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����C����1��2������|2a��b+8|+��a+b��2��2��0��

��1����a��b��ֵ��
��2����ͼ1����G��y���ϣ�������COG�������������ABC�������![]() �������G�����ꣻ
�������G�����ꣻ
��3����ͼ2������C��CD��y�ύy���ڵ�D����PΪ�߶�CD�ӳ����ϵ�һ�����㣬����OP��AC��DB��OEƽ�֡�AOP��OF��CE������OPD+k��DOF��k����FOP+��AOE�����ֽ��ı���ABDC����ƽ��![]() k����λ�õ��ı���A1B1D1C1����֪AM+BN =
k����λ�õ��ı���A1B1D1C1����֪AM+BN =![]() k����ͼ����Ӱ���ֵ������
k����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
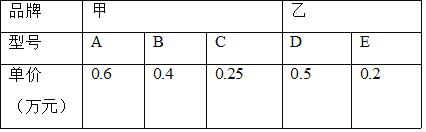
����Ŀ��һ�̳���A��B��C�����ͺŵļ�Ʒ�Ƶ��Ժ�D��E�����ͺŵ���Ʒ�Ƶ��ԣ�ij��ѧ���Ӽס�������Ʒ�Ƶĵ����и�ѡ��һ���ͺŵĵ���װ��������ң�
��1��д������ѡ��������������״ͼ���б�����ʾ����
��2������1���и���ѡ��������ѡ�еĿ�������ͬ����ôA�ͺű�ѡ�еĸ����Ƕ��٣�
��3����֪����ѧ��18��Ԫ����ҹ���ס�������Ʒ�Ƶ��Ըպ�32̨���۸����±���ʾ����λ����Ԫ�������м�Ʒ�Ƶ���ѡΪA�ͺţ������ѧ����A�ͺŵ��Զ���̨��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com