
【题目】如图,等腰三角形![]() 的一边
的一边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,
,![]() ,动点
,动点![]() 从原点
从原点![]() 出发,在线段
出发,在线段![]() 上以每秒2个单位的速度向点
上以每秒2个单位的速度向点![]() 匀速运动,动点
匀速运动,动点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴的正半轴以每秒1个单位的速度向上匀速运动,过点
轴的正半轴以每秒1个单位的速度向上匀速运动,过点![]() 作
作![]() 轴的平行线分别交
轴的平行线分别交![]() 于
于![]() ,设动点
,设动点![]() ,
,![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,点
时,点![]() 也停止运动,他们运动的时间为
也停止运动,他们运动的时间为![]() 秒
秒![]() .
.

(1)点![]() 的坐标为_____,
的坐标为_____,![]() 的坐标为____;
的坐标为____;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(3)是否存在某一时刻![]() ,使
,使![]() 为直角三角形?若存在,请求出此时
为直角三角形?若存在,请求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)(![]() t,t),(10-
t,t),(10-![]() t,t);(2)当t为
t,t);(2)当t为![]() 时,四边形POEF是平行四边形;(3)t=
时,四边形POEF是平行四边形;(3)t=![]() 和4时,使△PEF为直角三角形.
和4时,使△PEF为直角三角形.
【解析】
(1)过点A作AD⊥OB,由点A的坐标为(6,8),可得OD=6,AD=8,然后由勾股定理得:OA=10,由OA=OB可得:OB=10,进而可得:BD=4,进而可得点B的坐标为:(10,0),然后设OA的关系式:y=kx,然后将A(6,8)代入即可得直线OA的关系式,然后设直线AB的关系式为:y=kx+b,然后将A,B两点代入,即可确定直线AB的关系式,由过点Q作x轴的平行线分别交OA,AB于E,F,可知点Q、E、F三点的纵坐标相等均为t,然后由点E在OA上,点F在AB上,将点E、F的纵坐标分别代入对应的关系式,即可得到得到点E、F的坐标;
(2)由EF∥OP,欲使四边形POEF是平行四边形,只需EF=OP即可,从而可得关于t的等式,解答即可;
(3)分三种情况讨论:①PE⊥EF,②PE⊥PF,③EF⊥PF即可.
解:(1)过点A作AD⊥OB,垂足为D,如图1,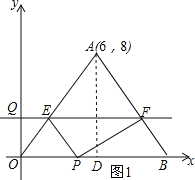
∵点A的坐标为(6,8),
∴OD=6,AD=8,
由勾股定理得:OA=10,
∵OA=OB,
∴OB=10,
∴BD=4,
∴点B的坐标为:(10,0),
设直线OA的关系式:y=kx,
将A(6,8)代入上式,得:
6k=8,
解得:k=![]() ,
,
所以直线OA的关系式:y=![]() x,
x,
设直线AB的关系式为:y=kx+b,
将A,B两点代入上式得: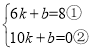 ,
,
解得:![]() ,
,
所以直线AB的关系式为:y=-2x+20,
∵过点Q作x轴的平行线分别交OA,AB于E,F,
∴点Q、E、F三点的纵坐标相等,
∵动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,
动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,
∴t秒后,OQ=t,OP=2t,
∴Q、E、F三点的纵坐标均为t,
将点E的纵坐标t代入y=![]() x,得:x=
x,得:x=![]() t,
t,
∴E点的坐标为:(![]() t,t),
t,t),
将点E的纵坐标t代入y=-2x+20,得:x=10-![]() t,
t,
∴F点的坐标为:(10-![]() t,t),
t,t),
故答案为:(![]() t,t),(10-
t,t),(10-![]() t,t);
t,t);
(2)由(1)知:E(![]() t,t),F(10-
t,t),F(10-![]() t,t),
t,t),
∴EF=10-![]() t-
t-![]() t=10-
t=10-![]() t,
t,
∵四边形POEF是平行四边形,
∴EF∥OP,且EF=OP,
即10-![]() t=2t,
t=2t,
解得:t=![]() ,
,
∴当t为![]() 时,四边形POEF是平行四边形;
时,四边形POEF是平行四边形;
(3)过点E作EM⊥OB,垂足为M,过点F作FN⊥OB,垂足为N,
可得四边形EMNF是矩形,如图2,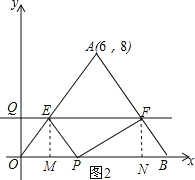
①当PE⊥PF时,PE2+PF2=EF2,
由(1)知:OM=![]() t,EM=FN=t,ON=10-
t,EM=FN=t,ON=10-![]() t,EF=10-
t,EF=10-![]() t,
t,
∴PM=![]() t,PN=10-
t,PN=10-![]() t,
t,
∵PE2=ME2+MP2,PF2=PN2+FN2,
∴t2+(![]() t)2+(10-
t)2+(10-![]() t)2+t2=(10-
t)2+t2=(10-![]() t)2,
t)2,
解得:t1=0(舍去),t2=![]() ;
;
②当PE⊥EF时,如图3,可得四边形EPNF是矩形,
∵四边形EPNF是矩形,
∴EF=PN,
即:EF=ON-OP,
∴10-![]() t=10-
t=10-![]() t-2t,
t-2t,
解得t=0(舍去);
③当EF⊥PF时,如图4,可得四边形EMPF是矩形,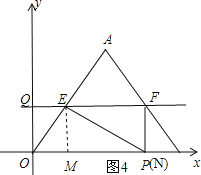
∵四边形EMPF是矩形,
∴EF=MP,
即EF=OP-OM,
∴10-![]() t=2t-
t=2t-![]() t,
t,
解得:t=4,
∴当t=![]() 和4时,使△PEF为直角三角形.
和4时,使△PEF为直角三角形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,把点
,把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 且与
且与![]() 平行的直线交
平行的直线交![]() 轴于点
轴于点![]() .
.
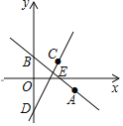
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1 240元,3辆甲种客车和2辆乙种客车共需租金1 760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了援助失学儿童,李明同学从2017年1月份开始,每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内,准备到2018年12月底一次性将储蓄盒内存款一并汇出.已知2017年2月份存款后清点储蓄盒内有存款260元,2017年5月份存款后清点储蓄盒内有350元.
(1)在李明2017年1月份存款前,储蓄盒内原有存款多少元?
(2)为了实现到2018年6月份存款后存款总数超过800元的目标,李明计划从2018年1月份开始,每月存款都比2017年每月存款多t(t为整数)元,求t的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车早晨7∶00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B、C、D在同一条直线上),小明研究图像得到了以下结论:
①甲乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8∶00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8∶24,
其中,正确的结论是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
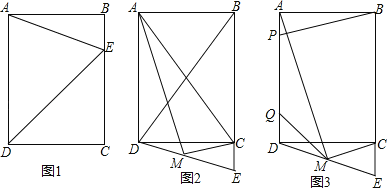
【题目】已知:如图,在矩形ABCD中,AB=6,BC=8,E为直线BC上一点.
(1)如图1,当E在线段BC上,且DE=AD时,求BE的长;
(2)如图2,点E为BC延长长线上一点,若BD=BE,连接DE,M为ED的中点,连接AM,CM,求证:AM⊥CM;
(3)如图3,在(2)条件下,P,Q为AD边上的两个动点,且PQ=5,连接PB、MQ、BM,求四边形PBMQ的周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com