
分析 首先估算$\sqrt{7}$和$\sqrt{11}$的取值范围,精确到0.01,从而得出结论.
解答 解:∵2<$\sqrt{7}$<3,2.62=6.76,2.72=7.29,
∴2.6<$\sqrt{7}$<2.7,
∵2.642=6.9696,2.652=7.0225,
估计$\sqrt{7}$≈2.65
∵3$<\sqrt{11}<4$,3.32=10.89,3.42=11.56,
∴3.3$<\sqrt{11}$<3.4,
∵3.312=10.9561,3.322=11.0224,
估计$\sqrt{11}$≈3.32,
∴$\sqrt{7}$$+\sqrt{11}$≈5.97,
整数部分为5,
故答案为:5.
点评 此题主要考查了估计无理数大小,用“夹逼法”得出$\sqrt{7}$和$\sqrt{11}$的取值范围是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
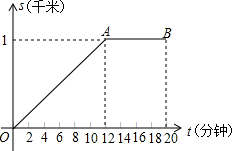 小亮早晨从家里出发匀速步行去上学,小亮的妈妈在小亮出发后10分钟,发现小亮的数学课本没带,于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮,结果与小亮同时到达学校.已知小亮在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA-AB所示.
小亮早晨从家里出发匀速步行去上学,小亮的妈妈在小亮出发后10分钟,发现小亮的数学课本没带,于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮,结果与小亮同时到达学校.已知小亮在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA-AB所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
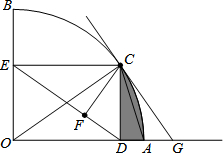 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点F在线段DE上,且EF=2DF,过点C的直线CG交OA的延长线于点G,且∠CGO=∠CDE.
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点F在线段DE上,且EF=2DF,过点C的直线CG交OA的延长线于点G,且∠CGO=∠CDE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
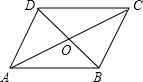 如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )| A. | 1<m<11 | B. | 2<m<22 | C. | 10<m<12 | D. | 5<m<6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com