
分析 对分母利用完全平方公式进行变形,然后再来计算结果.
解答 解:原式=$\frac{(200{2}^{2}-2001)•2003}{200{2}^{2}-2×2002•2001+200{1}^{2}+2002•2001}$
=$\frac{(200{2}^{2}-2001)•2003}{(2002-2001)^{2}+2002•2001}$
=$\frac{(200{2}^{2}-2001)•2003}{1+2002(2002-1)}$
=$\frac{(200{2}^{2}-2001)•2003}{200{2}^{2}-2001}$
=2003.
故答案为:2003.
点评 本题考查了利用公式变形进行化简计算,熟练的运用乘法公式变形是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
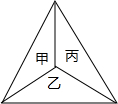 如图,一只蚊子在甲、乙、丙三个房间之间飞来飞去,蚊子从一个房间随机飞到另一个房间,共飞三次.
如图,一只蚊子在甲、乙、丙三个房间之间飞来飞去,蚊子从一个房间随机飞到另一个房间,共飞三次.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
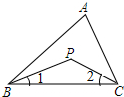 如图,P是△ABC内一点,连结PB、PC.
如图,P是△ABC内一点,连结PB、PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com