
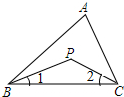
 ��ͼ��P�ǡ�ABC��һ�㣬����PB��PC��
��ͼ��P�ǡ�ABC��һ�㣬����PB��PC������ ��1������֪BP��CP�ֱ��ǡ�ABC���ACB��ƽ���ߣ����Ƴ���P=180��-��1-��2=180��-$\frac{1}{2}$����ABC+��ACB��=180��-$\frac{1}{2}$��180��-��A��=90��+$\frac{1}{2}$��A��
��2������1=$\frac{1}{3}$��ABC����2=$\frac{1}{3}$��ACBʱ����P=180��-��1-��2=180��-$\frac{1}{3}$����ABC+��ACB��=180��-$\frac{1}{3}$��180��-��A��=120��+��A��
��3������1=$\frac{1}{n}$��ABC����2=$\frac{1}{n}$��ACBʱ�����գ�3���ķ������ó����ۣ�
��� �⣺��1���������������£�
��1+��2=$\frac{1}{2}$��180��-��A��=90��-$\frac{1}{2}$��A��
��P=180��-����1+��2��=180��-��90��-$\frac{1}{2}$��A��=90��+$\frac{1}{2}$��A��
��2����P=120��+$\frac{1}{3}$��A��
�������£�
��1=$\frac{1}{3}$ABC����2=$\frac{1}{3}$��ACB��
��1+��2=$\frac{1}{3}$��180��-��A��=60��-$\frac{1}{3}$��A��
��P=180��-����1+��2��=180��-��60��-$\frac{1}{3}$��A��=120��+$\frac{1}{3}$��A��
��3����P=180��-$\frac{180��}{n}$+$\frac{1}{n}$��A��
�������£�
��1=$\frac{1}{n}$ABC����2=$\frac{1}{n}$��ACB��
��1+��2=$\frac{1}{n}$��180��-��A����
��P=180��-����1+��2��=180��-$\frac{180��}{n}$+$\frac{1}{n}$��A��
���� ���⿼������������ڽǺͶ����ͽ�ƽ���ߵĶ��壬�����������ڽǺ͵���180���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
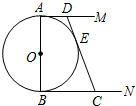 ��ͼ����O��ֱ��AB=2��AM��BN�������������ߣ�DE�С�O��E����AM��D����BN ��C����AD=x��BC=y��
��ͼ����O��ֱ��AB=2��AM��BN�������������ߣ�DE�С�O��E����AM��D����BN ��C����AD=x��BC=y�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3m-n}{n+m}$ | B�� | -$\frac{3m-n}{n+m}$ | C�� | $\frac{m-n}{m+n}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
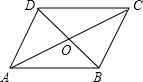 ��ͼ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O�����AC=12��BD=10��AB=m����ôm��ȡֵ��Χ�ǣ�������
��ͼ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O�����AC=12��BD=10��AB=m����ôm��ȡֵ��Χ�ǣ�������| A�� | 1��m��11 | B�� | 2��m��22 | C�� | 10��m��12 | D�� | 5��m��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com