练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某厂家为了解销售轿车台数与广告宣传费之间的关系，得到如表统计数据表：根据数据表可得回归直线方程 ，其中 ， ，据此模型预测广告费用为9万元时，销售轿车台数为（ ）

    广告费用x（万元）

    2

    3

    4

    5

    6

    销售轿车y（台数）

    3

    4

    6

    10

    12


    A.17
    B.18
    C.19
    D.20

    【答案】C
    【解析】解：根据表中数据，计算 = ×（2+3+4+5+6）=4，
    = ×（3+4+6+10+12）=7，
    且回归直线方程为 =2.4x+ ，
    ∴ =7﹣2.4×4=﹣2.6，
    ∴回归方程为 =2.4x﹣2.6；
    当x=9时， =2.4×9﹣2.6=19，
    即据此模型预测广告费用为9万元时，销售轿车台数为19．
    故选：C．
    根据表中数据计算 、 ，由回归直线方程过样本中心点求出 的值，写出回归方程，利用回归方程计算x=9时 的值即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在四棱柱ABCD﹣A1B1C1D1中，四边形ABCD为平行四边形，AA1⊥平面ABCD，∠BAD=60°，AB=2，BC=1．AA1= ，E为A1B1的中点．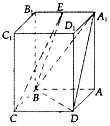
    （1）求证：平面A1BD⊥平面A1AD；
    （2）求多面体A1E﹣ABCD的体积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙三人投掷飞镖，他们的成绩（环数）如下面的频数条统计图所示．则甲、乙、丙三人的训练成绩方差S甲2 ， S乙2 ， S丙2的大小关系是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知曲线C上任意一点M到点F（0，1）的距离比它到直线l：y=﹣2的距离小1． （Ⅰ）求曲线C的方程；
    （Ⅱ）斜率不为0且过点P（2，2）的直线m与曲线C交于A，B两点，设 =λ ，当△AOB的面积为4 时（O为坐标原点），求λ的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“新零售”模式的背景下，某大型零售公司为推广线下分店，计划在S市的A区开设分店．为了确定在该区开设分店的个数，该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格．记x表示在各区开设分店的个数，y表示这x个分店的年收入之和．

    x（个）

    2

    3

    4

    5

    6

    y（百万元）

    2.5

    3

    4

    4.5

    6

    （Ⅰ）该公司已经过初步判断，可用线性回归模型拟合y与x的关系，求y关于x的线性回归方程y= ；
    （Ⅱ）假设该公司在A区获得的总年利润z（单位：百万元）与x，y之间的关系为z=y﹣0.05x2﹣1.4，请结合（Ⅰ）中的线性回归方程，估算该公司应在A区开设多少个分店时，才能使A区平均每个分店的年利润最大？
    参考公式： = x+a， = = ，a= ﹣ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线E：y2=x与圆M：（x﹣4）2+y2=r2（r＞0）相交于A、B、C、D四个点．
    （Ⅰ）求r的取值范围；
    （Ⅱ）当四边形ABCD的面积最大时，求对角线AC、BD的交点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面给出四种说法： ①用相关指数R2来刻画回归效果，R2越小，说明模型的拟合效果越好；
    ②命题P：“x0∈R，x02﹣x0﹣1＞0”的否定是￢P：“x∈R，x2﹣x﹣1≤0”；
    ③设随机变量X服从正态分布N（0，1），若P（x＞1）=p，则P（﹣1＜X＜0）= ﹣p
    ④回归直线一定过样本点的中心（ ， ）．
    其中正确的说法有（请将你认为正确的说法的序号全部填写在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，侧面ABB1A1为矩形，AB= ，AA1=2，D为AA1的中点，BD与AB1交于点O，CO⊥侧面ABB1A1 ．
    （1）证明：CD⊥AB1；
    （2）若OC=OA，求直线C1D与平面ABC所成角的正弦值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（列方程（组）及不等式解应用题）
    春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．
    （1）求甲、乙两种商品每件的进价分别是多少元？
    （2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

    查看答案和解析>>

    同步练习册答案