
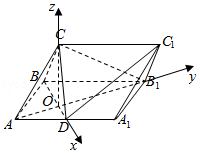
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB= ![]() ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
【答案】
(1)证明:由题意可知,在Rt△ABD中,tan∠ABD= ![]() =
= ![]() ,
,
在Rt△ABB1中,tan∠AB1B= ![]() =
= ![]() .
.
又因为0<∠ABD,∠AB1B ![]() ,所以∠ABD=∠AB1B,
,所以∠ABD=∠AB1B,
所以∠ABD+∠BAB1=∠AB1B+∠BAB1= ![]() ,
,
所以AB1⊥BD.
又CO⊥侧面ABB1A1,且AB1侧面ABB1A1,∴AB1⊥CO.又BD与CO交于点O,所以AB1⊥平面CBD.
又因为BC平面CBD,所以BC⊥AB1.
(2)解:如图所示,以O为原点,分别以OD,OB1,OC所在的直线为x轴,y轴,z轴,建立空间直角坐标系,
则A(0,﹣ ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0,0),C(0,0,
,0,0),C(0,0, ![]() ),
),
B1(0, ![]() ,0),D(
,0),D( ![]() ,0,0).
,0,0).
又因为 ![]() =2
=2 ![]() ,所以C1(
,所以C1( ![]() ,
, ![]() ,
, ![]() ).
).
所以 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ).
).
设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则由  ,得
,得 
令y= ![]() ,则z=﹣
,则z=﹣ ![]() ,x=1,
,x=1, ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() )是平面ABC的一个法向量.
)是平面ABC的一个法向量.
设直线C1D与平面ABC所成的角为α,
则sin α=  =
= ![]() .
.
故直线C1D与平面ABC所成角的正弦值为 ![]() .
.
【解析】(1)推导出∠ABD=∠AB1B,从而∠ABD+∠BAB1=∠AB1B+∠BAB1= ![]() ,进而AB1⊥BD.由线面垂直得AB1⊥CO.从而AB1⊥平面CBD.由此能证明BC⊥AB1 . (2)以O为原点,分别以OD,OB1 , OC所在的直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出直线C1D与平面ABC所成角的正弦值.
,进而AB1⊥BD.由线面垂直得AB1⊥CO.从而AB1⊥平面CBD.由此能证明BC⊥AB1 . (2)以O为原点,分别以OD,OB1 , OC所在的直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出直线C1D与平面ABC所成角的正弦值.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】设函数f(x)=x3﹣2ex2+mx﹣lnx,记g(x)= ![]() ,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
A.(﹣∞,e2+ ![]() ]
]
B.(0,e2+ ![]() ]
]
C.(e2+ ![]() ,+∞]
,+∞]
D.(﹣e2﹣ ![]() ,e2+
,e2+ ![]() ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家为了解销售轿车台数与广告宣传费之间的关系,得到如表统计数据表:根据数据表可得回归直线方程 ![]() ,其中
,其中 ![]() ,
, ![]() ,据此模型预测广告费用为9万元时,销售轿车台数为( )
,据此模型预测广告费用为9万元时,销售轿车台数为( )
广告费用x(万元) | 2 | 3 | 4 | 5 | 6 |
销售轿车y(台数) | 3 | 4 | 6 | 10 | 12 |
A.17
B.18
C.19
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示: 
(1)据此直方图,估算交通指数T∈[3,9)时的中位数和平均数;
(2)据此直方图,求市区早高峰马路之间的3个路段至少有2个严重拥堵的概率;
(3)某人上班路上所用时间,若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟;中度拥堵为45分钟;严重拥堵为60分钟,求此人上班所用时间的数学期望.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x+a|, ![]()
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)若a>﹣1,且当x∈[﹣a,1]时,不等式f(x)≤g(x)有解,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B的大小;
(2)已知b= ![]() ,BD为AC边上的高,求BD的取值范围.
,BD为AC边上的高,求BD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ① ![]() =
= ![]() ;②
;② ![]() =
= ![]() ;③
;③ ![]() ;④
;④ ![]() =
= ![]()
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com