
【题目】设函数f(x)=x3﹣2ex2+mx﹣lnx,记g(x)= ![]() ,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
A.(﹣∞,e2+ ![]() ]
]
B.(0,e2+ ![]() ]
]
C.(e2+ ![]() ,+∞]
,+∞]
D.(﹣e2﹣ ![]() ,e2+
,e2+ ![]() ]
]
【答案】A
【解析】解:∵f(x)=x3﹣2ex2+mx﹣lnx的定义域为(0,+∞), 又∵g(x)= ![]() ,
,
∴函数g(x)至少存在一个零点可化为
函数f(x)=x3﹣2ex2+mx﹣lnx至少有一个零点;
即方程x3﹣2ex2+mx﹣lnx=0有解,
则m= ![]() =﹣x2+2ex+
=﹣x2+2ex+ ![]() ,
,
m′=﹣2x+2e+ ![]() =﹣2(x﹣e)+
=﹣2(x﹣e)+ ![]() ;
;
故当x∈(0,e)时,m′>0,
当x∈(e,+∞)时,m′<0;
则m=﹣x2+2ex+ ![]() 在(0,e)上单调递增,
在(0,e)上单调递增,
在(e,+∞)上单调递减,
故m≤﹣e2+2ee+ ![]() =e2+
=e2+ ![]() ;
;
又∵当x+→0时,m=﹣x2+2ex+ ![]() →﹣∞,
→﹣∞,
故m≤e2+ ![]() ;
;
故选A.
由题意先求函数的定义域,再化简为方程x3﹣2ex2+mx﹣lnx=0有解,则m= ![]() =﹣x2+2ex+
=﹣x2+2ex+ ![]() ,求导求函数m=﹣x2+2ex+
,求导求函数m=﹣x2+2ex+ ![]() 的值域,从而得m的取值范围.
的值域,从而得m的取值范围.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC. 
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为平行四边形,AA1⊥平面ABCD,∠BAD=60°,AB=2,BC=1.AA1= ![]() ,E为A1B1的中点.
,E为A1B1的中点. 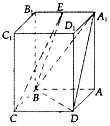
(1)求证:平面A1BD⊥平面A1AD;
(2)求多面体A1E﹣ABCD的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|+|x﹣3|,g(x)=a﹣|x﹣2|. (Ⅰ)若关于x的不等式f(x)<g(x)有解,求实数a的取值范围;
(Ⅱ)若关于x的不等式f(x)<g(x)的解集为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax2 , a>0.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点. (Ⅰ)求P点的轨迹C的方程;
(Ⅱ)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,若kEGkFH=﹣ ![]() ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人投掷飞镖,他们的成绩(环数)如下面的频数条统计图所示.则甲、乙、丙三人的训练成绩方差S甲2 , S乙2 , S丙2的大小关系是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=﹣2的距离小1. (Ⅰ)求曲线C的方程;
(Ⅱ)斜率不为0且过点P(2,2)的直线m与曲线C交于A,B两点,设 ![]() =λ
=λ ![]() ,当△AOB的面积为4
,当△AOB的面积为4 ![]() 时(O为坐标原点),求λ的值.
时(O为坐标原点),求λ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB= ![]() ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com