
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连结BD,DP,BD与CF相交于点H.给出下列结论: ①△ABE≌△DCF;②△DPH是等腰三角形;③PF= ![]() AB;④
AB;④ ![]() =
= ![]() .
.
其中正确结论的个数是( )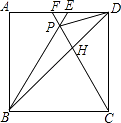
A.1
B.2
C.3
D.4
【答案】D
【解析】解:∵△BPC是等边三角形, ∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
在△ABE与△CDF中,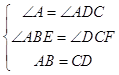 ,
,
∴△ABE≌△DCF,故①正确;
∵PC=DC,∠PCD=30°,
∴∠CPD=75°,
∵∠DBC=45°,∠BCF=60°,
∴∠DHP=∠BHC=75°,
∴PD=DH,
∴△DPH是等腰三角形,故②正确;
∵△BPC是等边三角形,
∴可得∠FPE=∠PFE=60°,
∴△FEP是等边三角形,
∴△FPE∽△CPB,
∴ ![]() =
= ![]() ,
,
设PF=x,PC=y,则DC=y,
∵∠FCD=30°,
∴y= ![]() (x+y),
(x+y),
整理得:(1﹣ ![]() )y=
)y= ![]() x,
x,
解得: ![]() =
= ![]() ,
,
则PF= ![]() AB,故③正确;
AB,故③正确;
如图,过P作PM⊥CD,PN⊥BC,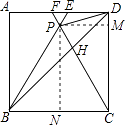
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴PN=PBsin60°=4× ![]() =2
=2 ![]() ,PM=PCsin30°=2,
,PM=PCsin30°=2,
S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD
= ![]() ×4×2
×4×2 ![]() +
+ ![]() ×2×4﹣
×2×4﹣ ![]() ×4×4
×4×4
=4 ![]() +4﹣8=4
+4﹣8=4 ![]() ﹣4,
﹣4,
∴ ![]() =
= ![]() ,故④正确;
,故④正确;
故正确的有4个,
故选:D.


科目:初中数学 来源: 题型:
【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系,QE与QF的数量关系.
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.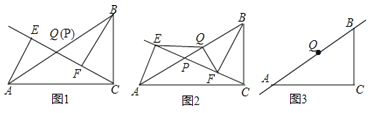
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( )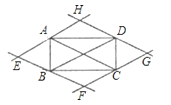
A.平行四边形
B.矩形
C.菱形
D.正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
(1)求证:AD=CE.
(2)若DE=3,CE=4,求tan∠DAE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
A.20%
B.40%
C.﹣220%
D.30%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.请在给出的5×5的正方形网格中,以格点为顶点,画出两个三角形,一个三角形的长分别是 ![]() 、2、
、2、 ![]() ,另一个三角形的三边长分别是
,另一个三角形的三边长分别是 ![]() 、2
、2 ![]() 、5
、5 ![]() .(画出的两个三角形除顶点和边可以重合外,其余部分不能重合)
.(画出的两个三角形除顶点和边可以重合外,其余部分不能重合) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点. 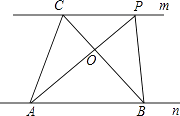
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com