
����Ŀ����֪����P��Rt��ABCб��AB��һ���㣨����A��B�غϣ����ֱ��A��B��ֱ��CP�����ߣ�����ֱ�ΪE��F��QΪб��AB���е㣮
��1����ͼ1������P���Q�غ�ʱ��AE��BF��λ�ù�ϵ��QE��QF��������ϵ.
��2����ͼ2������P���߶�AB�ϲ����Q�غ�ʱ�����ж�QE��QF��������ϵ��������֤����
��3����ͼ3������P���߶�BA����AB�����ӳ�����ʱ����ʱ��2���еĽ����Ƿ�������뻭��ͼ�β�����֤����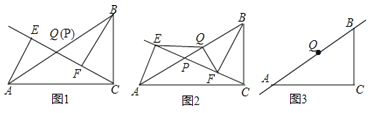
���𰸡��⣺��1����ͼ1��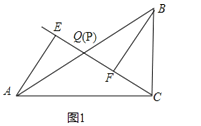
����P���Q�غ�ʱ��AE��BF��λ�ù�ϵ��AE��BF��QE��QF��������ϵ��AE=BF��
�����ǣ���QΪAB���е㣬
��AQ=BQ��
��AE��CQ��BF��CQ��
��AE��BF����AEQ=��BFQ=90�㣬
�ڡ�AEQ�͡�BFQ��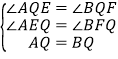
���AEQ�ա�BFQ��
��QE=QF��
�ʴ�Ϊ��AE��BF��QE=QF��
��2��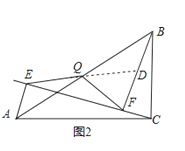
QE=QF��
֤�����ӳ�EQ��BF��D��
���ɣ�1��֪��AE��BF��
���AEQ=��BDQ��
�ڡ�AEQ�͡�BDQ��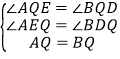
���AEQ�ա�BDQ��
��EQ=DQ��
�ߡ�BFE=90�㣬
��QE=QF����
��3������P���߶�BA����AB�����ӳ�����ʱ����ʱ��2���еĽ��۳�����
֤�����ӳ�EQ��FB��D����ͼ3��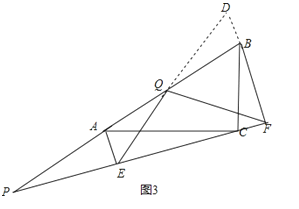
���ɣ�1��֪��AE��BF��
���AEQ=��BDQ��
�ڡ�AEQ�͡�BDQ��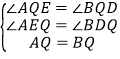
���AEQ�ա�BDQ��
��EQ=DQ��
�ߡ�BFE=90�㣬
��QE=QF��
����������1������AAS�Ƴ���AEQ�ա�BFQ���Ƴ�AE=BF���ɣ�
��2���ӳ�EQ��BF��D�������AEQ�ա�BDQ������ȫ�������ε����ʵó�EQ=QD������ֱ��������б�����е����ʵó����ɣ�
��3���ӳ�EQ��FB��D�������AEQ�ա�BDQ������ȫ�������ε����ʵó�EQ=QD������ֱ��������б�����е����ʵó����ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬѧ���ڿ���ʱ����֯����ͬѧ�μӵ���������ѵ����ԭ�����������ƹ������300Ԫ�������������ӵ�ԭ��������2���������Żݺ�һ��ֻ��480Ԫ���μӻ��ÿ��ͬѧƽ����̯�ķ��ñ�ԭ�ƻ���4Ԫ����ԭ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�� ��ABC����ACB�����ȷ��߽��ڵ�E��D������BFC=132�㣬��BGC=118�㣬���A�Ķ���Ϊ�� ��
A.65��
B.66��
C.70��
D.78��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0��������˵������abc��0����2a��b=0����4a+2b+c��0����������5��y1������![]() ��y2���������������㣬��y1��y2��
��y2���������������㣬��y1��y2��
����˵����ȷ���ǣ�������

A. �٢� B. �ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����xy2��x+y��3+x��x+y��2�Ĺ���ʽ��__��
��2��4x��m��n��+8y��n��m��2�Ĺ���ʽ��__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�����ֽƬ��һ��ֱ��������ֽƬ(��EFG��90��)����ͼ��ʾ��λ�ðڷţ�
ʹֱ��������ֽƬ��һ������Eǡ�����ڳ�����ֽƬ��һ��AB�ϣ���֪��BEF��21�㣬��
��CMF�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���BPC�ǵȱ������Σ�BP��CP���ӳ��߷ֱ�AD�ڵ�E��F������BD��DP��BD��CF�ཻ�ڵ�H���������н��ۣ� �١�ABE�ա�DCF���ڡ�DPH�ǵ��������Σ���PF= ![]() AB����
AB���� ![]() =
= ![]() ��
��
������ȷ���۵ĸ����ǣ� ��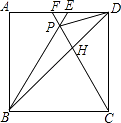
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com