
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论: ①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2﹣4ac=﹣12a;
④若m﹣n=﹣5,则B点坐标为(4,0)
其中正确的是( )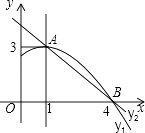
A.①
B.①②
C.①②③
D.①②③④
【答案】D
【解析】解:∵由图象可知,当x<1时,有y1<y2 , 故①正确; ∵抛物线的顶点坐标A(1,3),直线y2=mx+n(m≠0)经过A点,
∴当x=1时,y1=y2 ,
∴a+b+c=m+n,故②正确;
∵抛物线的最大值为 ![]() =3,
=3,
∴4ac﹣b2=12a,
∴b2﹣4ac=﹣12a,故③正确;
∵抛物线经过A(1,3),
∴代入y2=mx+n得,m+n=3,
解 ![]() 得
得 ![]() ,
,
∴y2=﹣x+4,
令y=0,则x=4,
∴B(4,0),故④正确;
故选D.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x﹣c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE 
(1)求证:DEAB=ACBE;
(2)如果AC2=ADAB,求证:AE=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. 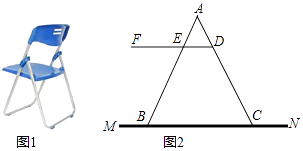
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)用配方法解一元二次方程:x2﹣6x+4=0.
(2)已知关于x的一元二次方程x2﹣4x+m=0的根的判别式的值为4,求m值及方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com