
【题目】某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
【答案】
(1)解:设需要搭配x个A种造型,则需要搭配B种造型(60﹣x)个,
则有 ![]() ,
,
解得37≤x≤40,
所以x=37或38或39或40.
第一种方案:A种造型37个,B种造型23个;
第二种方案:A种造型38个,B种造型22个;
第三种方案:A种造型39个,B种造型21个.
第四种方案:A种造型40个,B种造型20个;
(2)解:分别计算四种方案的成本为:
①37×600+23×800=40600元,
②38×600+22×800=40400元,
③39×600+21×800=40200元,
④40×600+20×800=40000元.
通过比较可知第④种方案成本最低.
答:选择第四种方案成本最低,最低为40000元
【解析】(1)设需要搭配x个A种造型,则需要搭配B种造型(60﹣x)个,根据“4200盆甲种花卉”“3090盆乙种花卉”列不等式求解,取整数值即可.(2)计算出每种方案的花费,然后即可判断出答案.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼,其高度仅次于世界排名第一的阿联酋迪拜大厦,某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°.已知东方明珠与上海中心大厦的水平距离约为900米,那么上海中心大厦的高度约为米(精确到1米).(参考数据:sin22.3°≈0.38,cos22.3°≈0.93.tan22.3°≈0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣1 | 0 | 2 | 3 | 4 | … |
y | … | 5 | 2 | 2 | 5 | 10 | … |
(1)根据上表填空: ①这个抛物线的对称轴是 , 抛物线一定会经过点(﹣2,);
②抛物线在对称轴右侧部分是(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论: ①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2﹣4ac=﹣12a;
④若m﹣n=﹣5,则B点坐标为(4,0)
其中正确的是( )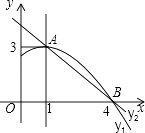
A.①
B.①②
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y= ![]() (x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( ) 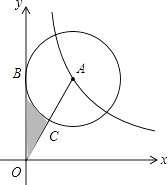
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农业现代化是我国“十三五”的重要规划之一,某地农民积极响应政府号召,自发成立现代新型农业合作社,适度扩大玉米种业规模,今年,合作社600亩玉米喜获丰收.合作社打算雇佣玉米收割机收割玉米,现有A,B两种型号收割机可供选择,且每台B种型号收割机每天的收个亩数是A种型号的1.5倍,如果单独使用一台收割机将600亩玉米全部收割完,A种型号收割机比B种型号收割机多用10天. 
(1)求A,B两种型号收割机每台每天收个玉米的亩数;
(2)已知A种型号收割机收费是45元/亩,B种型号收割机收费是50元/亩,经过研究,合作社计划同时雇佣A,B两种型号收割机各一台合作完成600亩玉米的收割任务,则合作社需要支付的玉米收割总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠ACB=110°,则∠P的度数是( ) 
A.55°
B.30°
C.35°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= ![]() ,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.
,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)求AP:PC的值;
(3)观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程平分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com