练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果x2+mx﹣12=（x+3）（x+n），那么（　　）

    A．m=﹣1，n=﹣4       B．m=7，n=4       C．m=1，n=﹣4   D．m=﹣7，n=﹣4


    A【考点】因式分解-十字相乘法等．

    【分析】利用多项式乘法去括号，再利用多项式各部分对应相等，进而求出m，n的值．

    【解答】解：∵x2+mx﹣12=（x+3）（x+n），

    ∴x2+mx﹣12=x2+（3+n）x+3n，

    故，

    解得：．

    故选：A．

    【点评】此题主要考查了多项式乘法，正确得出关于m，n的等式是解题关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一元二次方程x2—2x=0的实数根是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形ABCD中，AD=2AB，E是AD边上一点，DE=AD（n为大于2的整数），连接BE，作BE的垂直平分线分别交AD，BC于点F，G，FG与BE的交点为O，连接BF和EG．

    （1）试判断四边形BFEG的形状，并说明理由；

    （2）当AB=a（a为常数），n=3时，求FG的长；

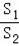
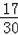
    （3）记四边形BFEG的面积为S1，矩形ABCD的面积为S2，当=时，求n的值．（直接写出结果，不必写出解答过程）

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形ABCD的边AB在x轴上，且AB的中点与原点重合，AB=2，AD=1，过定点Q（0，2）和动点P（a，0）的直线与矩形ABCD的边有公共点，则实数a的取值范围是　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线y=x2+bx﹣2的图象经过C点．

    （1）求抛物线的解析式；

    （2）平移该抛物线的对称轴所在直线l．当l移动到何处时，恰好将△ABC的面积分为相等的两部分？

    （3）点P是抛物线上一动点，是否存在点P，使四边形PACB为平行四边形？若存在，求出P点坐标；若不存在，说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC的内角∠ABC与外角∠ACD的平分线交于点E，且CE∥AB，AC与BE交于点E，则下列结论错误的是（　　）

    A．CB=CE     B．∠A=∠ECD     C．∠A=2∠E       D．AB=BF

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：（2x﹣3）2﹣2（3﹣x）（3+x）+9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知1是方程x=a－2x的解，则a=（  ）

    A. －1       B. 1     C.3       D.0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分式的值等于0时，x的值为（　　）

    A．x=±2 B．x=2   C．x=﹣2      D．x=

    　

    查看答案和解析>>

    同步练习册答案