
如图,△ABC的内角∠ABC与外角∠ACD的平分线交于点E,且CE∥AB,AC与BE交于点E,则下列结论错误的是( )


A.CB=CE B.∠A=∠ECD C.∠A=2∠E D.AB=BF
D【考点】三角形内角和定理;平行线的性质.
【分析】选项A和B:根据角平分线定义和平行线的性质推出∠FBC=∠E即可;选项C:先根据三角形外角的性质及角平分线的定义得出∠ACD=∠A+∠ABC,∠ECD=
 ∠ACD=
∠ACD=
 (∠A+∠ABC),再由BE平分∠ABC可知∠EBC=
(∠A+∠ABC),再由BE平分∠ABC可知∠EBC=
 ∠ABC,根据∠ECD是△BCE的外角即可得出结论;选项D:根据等腰三角形的判定和已知推出即可.
∠ABC,根据∠ECD是△BCE的外角即可得出结论;选项D:根据等腰三角形的判定和已知推出即可.
【解答】解:∵△ABC的内角∠ABC与外角∠ACD的平分线交于点E,
∴∠ABF=∠CBF,∠FCE=∠ECD,
∵CE∥AB,
∴∠A=∠FCE,∠E=∠ABE,
∴∠A=∠ECD,∠FBC=∠E,
∴CB=CE,
∵∠ACD=∠A+∠ABC,CE平分∠ACD,
∴∠ECD=
 ∠ACD=
∠ACD=
 (∠A+∠ABC)(角平分线的定义),
(∠A+∠ABC)(角平分线的定义),
∵BE平分∠ABC,
∴∠EBC=
 ∠ABC(角平分线的定义),
∠ABC(角平分线的定义),
∵∠ECD是△BCE的外角,
∴∠E=∠ECD﹣∠EBC=
 ∠A,
∠A,
即∠A=2∠E;
根据已知条件不能推出∠A=∠AFB,即不能推出AB=BF;
所以选项A、B、C的结论都正确,只有选项D的结论错误;
故选D.
【点评】本题考查的是三角形外角的性质,平行线的性质,等腰三角形的判定的应用,能综合运用知识点进行推理是解此题的关键.


科目:初中数学 来源: 题型:
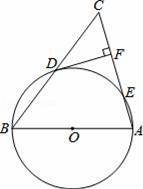
某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(2014•海淀区一模)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.
(1)求证:DF为⊙O的切线;
(2)若cosC=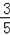
 ,CF=9,求AE的长.
,CF=9,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com