
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
 AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当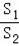
 =
=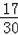
 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)


【考点】四边形综合题.
【专题】几何综合题.
【分析】(1)先求证△EFO≌△BGO,可得EF=BG,再根据△BOF≌△EOF,可得EF=BF;即可证明四边形BFEG为菱形;
(2)根据菱形面积不同的计算公式(底乘高和对角线乘积的一半两种计算方式)可计算FG的长度;
(3)根据菱形面积底乘高的计算方式可以求出BG长度,根据勾股定理可求出AF的长度,即可求出ED的长度,即可计算n的值.
【解答】解:(1)∵AD∥BC,
∴∠EFO=∠BGO,
∵FG为BE的垂直平分线,
∴BO=OE;
∵在△EFO和△BGO中,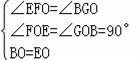
 ,
,
∴△EFO≌△BGO,
∴EF=BG,
∵AD∥BC,
∴四边形BGEF为平行四边形;
∵在△BOF和△EOF中,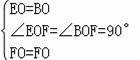
 ,
,
∴△BOF≌△EOF,
∴EF=BF,
∵邻边相等的平行四边形为菱形,
∴四边形BGEF为菱形.
(2)当AB=a,n=3时,AD=2a,AE=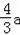
 ,
,
根据勾股定理可以计算BE=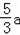
 ,
,
∵AF=AE﹣EF=AE﹣BF,在Rt△ABF中AB2+AF2=BF2,计算可得AF=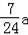
 ,EF=
,EF=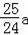
 ,
,
∵菱形BGEF面积=
 BE•FG=EF•AB,计算可得FG=
BE•FG=EF•AB,计算可得FG=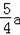
 .
.
(3)设AB=x,则DE=
 ,
,
S1=BG•AB,S2=BC•AB
当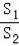
 =
=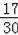
 时,
时,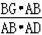
 =
=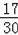
 ,可得BG=
,可得BG=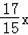
 ,
,
在Rt△ABF中AB2+AF2=BF2,计算可得AF=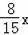
 ,
,
∴AE=AF+FE=AF+BG=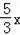
 ,DE=AD﹣AE=
,DE=AD﹣AE=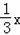
 ,
,
∴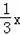
 =
=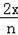
 ,
,
∴n=6.
【点评】牢记菱形的底乘高和对角线求面积的计算公式,熟练运用勾股定理才能解本题.


科目:初中数学 来源: 题型:
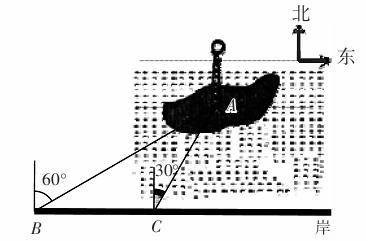
如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为
A.某人在岸边的B处测得A在B的北偏东60°的方向上.然后沿岸边直行200米到达C
处,再次测得4在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部
4到岸边BC的距离(结果精确到0.1米,
(参考数据: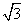 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知数轴上的点A对应的数为6,B是数轴上的一点,且AB=10,动点P从
点A出发,以每秒6个单位长度的速度沿着数轴向左匀速运动,设运动时间为t秒(t>0).
(1)数轴上点B对应的数是_______,点P对应的数是_______(用t的式子表示);
(2)动点Q从点B与点P同时出发,以每秒4个单位长度的速度沿着数轴向左匀速运动,试问:
运动多少时间点P可以追上点Q?
(3)M是AP的中点,N是PB的中点,点P在运动过程中,线段MN的长度是否发生变化?
若有变化,说明理由;若没有变化,请你画出图形,并求出MN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com