Question

如图，在直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线y=x²+bx﹣2的图象经过C点．

（1）求抛物线的解析式；

（2）平移该抛物线的对称轴所在直线l．当l移动到何处时，恰好将△ABC的面积分为相等的两部分？

（3）点P是抛物线上一动点，是否存在点P，使四边形PACB为平行四边形？若存在，求出P点坐标；若不存在，说明理由．

　

Answer 1

【考点】二次函数综合题．

【分析】（1）首先构造全等三角形△AOB≌△CDA，求出点C的坐标；然后利用点C的坐标求出抛物线的解析式；

（2）首先求出直线BC与AC的解析式，设直线l与BC、AC交于点E、F，则可求出EF的表达式；根据S_△CEF=S_△ABC，列出方程求出直线l的解析式；

（3）首先作出▱PACB，然后证明点P在抛物线上即可．

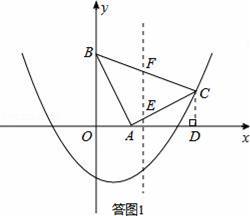
【解答】解：（1）如答图1所示，过点C作CD⊥x轴于点D，则∠CAD+∠ACD=90°．

∵∠OBA+∠OAB=90°，∠OAB+∠CAD=90°，

∴∠OAB=∠ACD，∠OBA=∠CAD．

∵在△AOB与△CDA中，

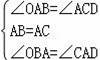
∴△AOB≌△CDA（ASA）．

∴CD=OA=1，AD=OB=2，

∴OD=OA+AD=3，

∴C（3，1）．

∵点C（3，1）在抛物线y=x²+bx﹣2上，

∴1=×9+3b﹣2，解得：b=﹣．

∴抛物线的解析式为：y=x²﹣x﹣2，

；

 

（2）在Rt△AOB中，OA=1，OB=2，由勾股定理得：AB=．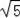

∴S_△ABC=AB²=．

设直线BC的解析式为y=kx+b，∵B（0，2），C（3，1），

∴，

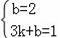
解得k=﹣，b=2，

∴y=﹣x+2．

同理求得直线AC的解析式为：y=x﹣．

如答图1所示，

设直线l与BC、AC分别交于点E、F，则EF=（﹣x+2）﹣（x﹣）=﹣x．

△CEF中，EF边上的高h=OD﹣x=3﹣x．

由题意得：S_△CEF=S_△ABC，

即： EF•h=S_△ABC，

∴×（﹣x）•（3﹣x）=×，

整理得：（3﹣x）²=3，

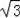
解得x=3﹣或x=3+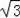（不合题意，舍去），

∴当直线l解析式为x=3﹣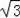时，恰好将△ABC的面积分为相等的两部分．

 

（3）存在．

如答图2所示，

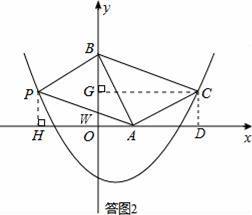
过点C作CG⊥y轴于点G，则CG=OD=3，OG=1，BG=OB﹣OG=1．

过点A作AP∥BC交y轴于点W，

∵四边形ACBP是平行四边形，

∴AP=BC，连接BP，则四边形PACB为平行四边形．

过点P作PH⊥x轴于点H，

∵BC∥AP，

∴∠CBO=∠AWO，

∵PH∥WO，

∴∠APH=∠AWO，

∴∠CBG=∠APH，

在△PAH和△BCG中，

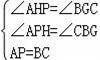
∴△PAH≌△BCG（AAS），

∴PH=BG=1，AH=CG=3，

∴OH=AH﹣OA=2，

∴P（﹣2，1）．

抛物线解析式为：y=x²﹣x﹣2，当x=﹣2时，y=1，即点P在抛物线上．

∴存在符合条件的点P，点P的坐标为（﹣2，1）．

【点评】本题考查了二次函数综合题型以及二次函数的图象与性质、一次函数的图象与性质、待定系数法、全等三角形、平行四边形、等腰直角三角形等知识点．试题难度不大，但需要仔细分析，认真计算．