
分析 根据算术平方根的定义:一个非负数的正的平方根,即为这个数的算术平方根;平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可求出结果.
解答 解:(1)$\sqrt{16}$=4;
(2)$\sqrt{0.04}$=0.2;
(3)$\sqrt{(-4)^{2}}$=4;
(4)$\sqrt{(-8)×(-2)}$=4;
(5)$\sqrt{1{3}^{2}-1{2}^{2}}$=5;
(6)$\sqrt{3600}$=60;
(7)$\sqrt{0.0001}$=0.01;
(8)-$\sqrt{\frac{9}{256}}$=-$\frac{3}{16}$;
(9)±$\sqrt{16}$=±4.
点评 此题考查了算术平方根和平方根,掌握算术平方根和平方根的定义是本题的关键;注意一个正数的平方根有2个,负数没有平方根.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
 已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
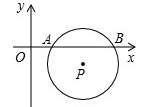 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=7,b=24,c=25 | B. | a=11,b=60,c=61 | C. | a=$\frac{8}{3}$,b=2,c=$\frac{13}{3}$ | D. | a=1,b=$\frac{5}{4}$,c=$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
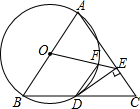 如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com