
【题目】已知二次函数![]() .
.
(1)求顶点坐标和对称轴方程;
(2)求该函数图象与x标轴的交点坐标;
(3)指出x为何值时,![]() ;当x为何值时,
;当x为何值时,![]() .
.
【答案】(1)y=x2-4x+3= x2-4x+4-1=(x-2)2-1
所以,抛物线的顶点坐标是(2,-1),对称轴方程为x=2.
(2)令y=0,得x2-4x+3=0,解得x1=1,x2=3,所以函数图象与x轴的交点坐标为(1,0),(3,0).
(3)当x<1,x>3时,y>0;当1<x<3时,y<0;
【解析】(1)根据二次函数的顶点坐标公式和对称轴公式分别求出即可;
(2)令y=0,得![]() , 解之即可;
, 解之即可;
(3)根据a的值及函数图象与x标轴的交点坐标,即可指出x为何值时,![]() ;当x为何值时,
;当x为何值时,![]() .
.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-1.5]=-2.
(1)[-π]= ;
(2)如果[a]=2,那么a的取值范围是 ;
(3)如果[![]() ]=-5,求满足条件的所有整数x;
]=-5,求满足条件的所有整数x;
(4)直接写出方程6x-3[x]+7=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(x,y),点B(x﹣my,mx﹣y)(其中m为常数,且m≠0),则称B是点A的“m族衍生点”.例如:点A(1,2)的“3族衍生点”B的坐标为(1﹣3×2,3×1﹣2),即B(﹣5,1).
(1)点(2,0)的“2族衍生点”的坐标为 ;
(2)若点A的“3族衍生点”B的坐标是(﹣1,5),则点A的坐标为 ;
(3)若点A(x,0)(其中x≠0),点A的“m族衍生点“为点B,且AB=OA,求m的值;
(4)若点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,则点A的位置在 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )
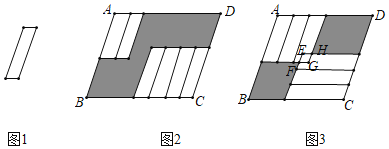
A.0.5B.1C.1.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某商场搞优惠促销活动,其活动内容是:“凡在本商场一次性购物超过100元者,超过100元的部分按9折优惠”.在此活动中,李明到该商场为单位一次性购买单价为60元的办公用品x(x>2)件,则应付款y(元)与商品件数x(件)之间的关系式是( )
A.y=54xB.y=54x+10
C.y=54x-90D.y=54x+45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),沿
重合),沿![]() 折叠该纸片,点
折叠该纸片,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() .
.

(1)如图1,当点![]() 在第一象限,且
在第一象限,且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当点![]() 为
为![]() 的中点时;
的中点时;
①求证:![]() ;
;
②直接写出四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△ ![]() 的位置,点B,O分别落在点
的位置,点B,O分别落在点 ![]() ,
, ![]() 处,点
处,点 ![]() 在
在 ![]() 轴上,再将△
轴上,再将△ ![]() 绕点
绕点 ![]() 顺时针旋转到△
顺时针旋转到△ ![]() 的位置,点
的位置,点 ![]() 在
在 ![]() 轴上,将△
轴上,将△ ![]() 绕点
绕点 ![]() 顺时针旋转△
顺时针旋转△ ![]() 的位置,点
的位置,点 ![]() 在
在 ![]() 轴上……依次进行下去。若点
轴上……依次进行下去。若点 ![]() ,B(0,2),则点
,B(0,2),则点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在函数![]() (x>0)的图象上,点B在直线
(x>0)的图象上,点B在直线![]() (k为常数,且k
(k为常数,且k![]() 0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.只有1对或2对
B.只有1对
C.只有2对
D.只有2对或3对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com