
����Ŀ����ƽ��ֱ������ϵ�У���֪��A(x��y)����B(x��my��mx��y)������mΪ��������m��0�������B�ǵ�A�ġ�m�������㡱�����磺��A(1��2)�ġ�3�������㡱B������Ϊ(1��3��2��3��1��2)����B(��5��1)��
��1���㣨2��0���ġ�2�������㡱������Ϊ�� ����
��2������A�ġ�3�������㡱B��������(��1��5)�����A������Ϊ�� ����
��3������A(x��0)������x��0������A�ġ�m�������㡰Ϊ��B����AB��OA����m��ֵ��
��4������A(x��y)�ġ�m�������㡱�롰��m�������㡱������y��Գƣ����A��λ������ ����
���𰸡���1��(2��4)����2��(2��1)����3��m����1����4��y����
��������
��1��������m�����������Ķ������⣻
��2�����A����Ϊ��x��y����������m�����������Ķ����г������飬������⣻
��3���������A����m����������Ϊ��B��x��mx������AB��OA������⣻
��4���������A��x��y������m����������Ϊ��x��my��mx��y������A��x��y��������m����������Ϊ��x+my����mx��y��������ԳƵ����ʿ���x��0��������⣮
�⣺��1���㣨2��0������2����������������Ϊ��2��2��0��2��2��0��������2��4����
�ʴ�Ϊ��2��4����
��2�����A������x��y����
������ɵã�![]() ��
��
��![]() ��
��
���A������2��1����
��3���ߵ�A��x��0����
���A����m������������B��x��mx����
��AB��|mx|��
��AB��OA��
��|x|��|mx|��
��m����1��
��4���ߵ�A��x��y����
���A��x��y������m������������x��my��mx��y������A��x��y��������m������������x+my����mx��y����
�ߵ�A��x��y������m����������������m����������������y��Գƣ�
��![]() ��
��
��x��0��
���A��y���ϣ�
�ʴ�Ϊ��y���ϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ����֪����ABC�У���BAC��40����BD��AC��D��CE��AB��E��BD��CE����ֱ�߽��ڵ�F������BFC�Ķ�����
��2���ڣ�1���Ļ����ϣ�����BACÿ������10�������ڱ仯��������ABC����ACBʼ�ձ�������ǣ�����t�루0��t��14��������BFC����BAC���������У���һ��Ϊ��һ��������ʱ����t��ֵ��
��3���ڣ�2���Ļ����ϣ���ABD����ACE�Ľ�ƽ���߽��ڵ�G����BGC�Ƿ�Ϊ��ֵ������ǣ���ֱ��д����BGC��ֵ��������ǣ���д����BGC����α仯�ģ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵġ�ABC �͡�DBE ��ͼ 1 ��ʽ�ڷţ����С�ACB����DEB��90������A����D��30������ E ���� AB �ϣ�DE ����ֱ�߽� AC ����ֱ���ڵ� F��
��1������ͼ 1 �еġ�DBE �Ƶ� B ��˳ʱ�뷽����ת�������� 0��������60���������������䣬��ͼ 2������ֱ��д���߶� AF��EF��DE ��������ϵ��
��2������ͼ 1 �еġ�DBE �Ƶ� B ��˳ʱ�뷽����ת�������� 60��ܦ¡�180���������������䣮
����ͼ 3����1�����߶� AF��EF��DE ��������ϵ�Ƿ���Ȼ����������������֤���ý��ۣ�������������д���µĽ��۲�֤����
����ͼ 4��AB �е�Ϊ M��BE �е�Ϊ N���� BC�� 2![]() ������ MN�������� ��ʱ��MN ����������ֵΪ ������ ��ֱ��д���𰸼��ɣ�
������ MN�������� ��ʱ��MN ����������ֵΪ ������ ��ֱ��д���𰸼��ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
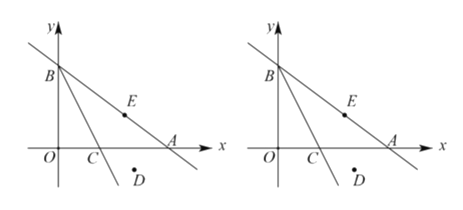
����Ŀ����ֱ֪��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ����ֱ��
����ֱ��![]() �ϣ��ۺ۽�
�ϣ��ۺ۽�![]() ���ڵ�
���ڵ�![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2������֪���������ڵĵ�![]() ����ֱ��
����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ���ı���
��ʹ���ı���![]() Ϊƽ���ı��Σ������ڣ������
Ϊƽ���ı��Σ������ڣ������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
��3���辭����![]() ����
����![]() �ᴹֱ��ֱ����ֱ��
�ᴹֱ��ֱ����ֱ��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P����������ABC�ڵ�һ�㣬��PA=6��PB=8��PC=10������APB�Ƶ�B��ʱ����תһ���ǶȺɵõ���CQB�� 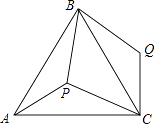
��1�����P���Q֮��ľ��룻
��2�����APB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ�� ![]() ����2�����ݵ�x��
����2�����ݵ�x�� ![]() ʱ��y��x���������С����a+b+c��0��ȷ���У� ��
ʱ��y��x���������С����a+b+c��0��ȷ���У� ��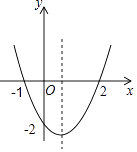
A.3��
B.4��
C.5��
D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() .
.
��1��������ͶԳ��᷽�̣�
��2����ú���ͼ����x����Ľ������ꣻ
��3��ָ��xΪ��ֵʱ��![]() ����xΪ��ֵʱ��
����xΪ��ֵʱ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߶�AB�Ƶ�A��ʱ����ת60���AC������BC������ABC�����Բ��O����PΪ�ӻ� ![]() �ϵ�һ�����㣬��AB��CP�ཻ�ڵ�D��
�ϵ�һ�����㣬��AB��CP�ཻ�ڵ�D�� 
��1�����APB�Ĵ�С��
��2������P�˶����δ�ʱ��PD��AB�������ʱCD��CP��ֵ��
��3���ڵ�P�˶������У��Ƚ�PC��AP+PB�Ĵ�С��ϵ�����Խ��۸���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��l��m���ȱߡ�ABC�Ķ���B��ֱ��m�ϣ���BC��ֱ��m�������Ϊ20�㣬��Ϧ��Ķ���Ϊ�� ��
A.60��![]()
B.45��
C.40��
D.30��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com