
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. 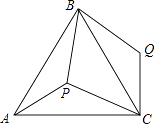
(1)求点P与点Q之间的距离;
(2)求∠APB的度数.
【答案】
(1)解:连接PQ,
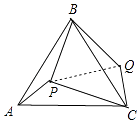
由旋转性质有:
BQ=BP=8,QC=PA=6,∠QBC=∠ABP,∠BQC=∠BPA,
∴∠QBC+∠PBC=∠ABP+∠PBC
即∠QBP=∠ABC,
∵△ABC是正三角形,
∴∠ABC=60°,
∴∠QBP=60°,
∴△BPQ是正三角形,
∴PQ=BP=BQ=8
(2)解:在△PQC中,PQ=8,QC=6,PC=10
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°
【解析】(1)由旋转的性质可以证明△PBQ是等边三角形,即可解决问题.(2)利用勾股定理的逆定理证明∠PQC=90°,由∠BQC=∠APB,即可解决问题.
【考点精析】掌握等边三角形的性质和勾股定理的逆定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成1块C型钢板、3块D型钢板;用1块B型钢板可制成2块C型钢板、1块D型钢板.
(1)现需150块C型钢板、180块D型钢板,则怡好用A型、B型钢板各多少块?
(2)若A、B型钢板共100块,现需C型钢板至多150块,D型钢板不超过204块,共有几种方案?
(3)若需C型钢板80块,D型钢板不多于45块(A型、B型钢板都要使用).求A、B型钢板各需多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
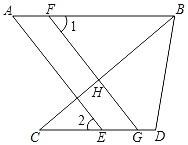
【题目】如图,点F在线段AB上,点E、G在线段CD上,AB∥CD.
(1)若BC平分∠ABD,∠D=100°,求∠ABC的度数.
解:∵AB∥CD(已知),
∴∠ABD+∠D=180°,( )
∵∠D=100°,(已知)
∴∠ABD= °,
∵BC平分∠ABD,(已知)
∴∠ABC=![]() ∠ABD=40°.(角平分线的定义)
∠ABD=40°.(角平分线的定义)
(2)若∠1=∠2,求证:AE∥FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(x,y),点B(x﹣my,mx﹣y)(其中m为常数,且m≠0),则称B是点A的“m族衍生点”.例如:点A(1,2)的“3族衍生点”B的坐标为(1﹣3×2,3×1﹣2),即B(﹣5,1).
(1)点(2,0)的“2族衍生点”的坐标为 ;
(2)若点A的“3族衍生点”B的坐标是(﹣1,5),则点A的坐标为 ;
(3)若点A(x,0)(其中x≠0),点A的“m族衍生点“为点B,且AB=OA,求m的值;
(4)若点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,则点A的位置在 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )
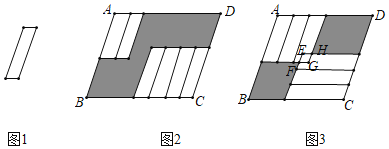
A.0.5B.1C.1.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),沿
重合),沿![]() 折叠该纸片,点
折叠该纸片,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() .
.

(1)如图1,当点![]() 在第一象限,且
在第一象限,且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当点![]() 为
为![]() 的中点时;
的中点时;
①求证:![]() ;
;
②直接写出四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“四月江南黄鸟肥,樱桃满市粲朝辉”,暮春时节,重庆市樱桃(俗称思桃儿)早已进入采摘期.某现代农业园区推行免入园费自助采摘活动.该园区种植了普通樱桃和乌皮樱桃两个品种,其中乌皮樱桃甜味香,肉质细嫩,售价比普通樱桃每斤高出20元.
(1)今年4月30日,普通樱桃销量为200斤,乌皮樱桃销量为400斤,若当天总销售额不低于26000元,则每斤普通樱桃至少卖多少元?
(2)为降低高温天气带来的经济损失,果园负责人决定在“五一”节推出优惠政策,若两种樱桃在(1)的条件下均以最低价格销售,5月1日,普通樱桃售价降低![]() ,销量比4月30日增加
,销量比4月30日增加![]() ,乌皮樱桃售价不变,销量比4月30日增加了
,乌皮樱桃售价不变,销量比4月30日增加了![]() ,且5月1日总销售额比4月30日增加了
,且5月1日总销售额比4月30日增加了![]() .求
.求![]() 的值.(
的值.(![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com