
����Ŀ�������½��ϻ���ʣ�ӣ�������ӳ�������ĺ��ʱ�ڣ�������ӣ�ң��׳�˼�Ҷ������ѽ����ժ�ڣ�ij�ִ�ũҵ������������������ժ���������ֲ����ͨӣ�Һ���Ƥӣ������Ʒ�֣�������Ƥӣ����ζ�㣬����ϸ�ۣ��ۼ۱���ͨӣ��ÿ��߳�20Ԫ��
��1������4��30�գ���ͨӣ������Ϊ200���Ƥӣ������Ϊ400������������۶����26000Ԫ����ÿ����ͨӣ������������Ԫ��
��2��Ϊ���������������ľ�����ʧ���������˾���������һ�����Ƴ��Ż����ߣ�������ӣ���ڣ�1���������¾�����ͼ۸����ۣ�5��1�գ���ͨӣ���ۼ۽���![]() ��������4��30������
��������4��30������![]() ����Ƥӣ���ۼ۲��䣬������4��30��������
����Ƥӣ���ۼ۲��䣬������4��30��������![]() ����5��1�������۶��4��30��������
����5��1�������۶��4��30��������![]() ����
����![]() ��ֵ����
��ֵ����![]() ����
����
���𰸡���1��30����2��30
��������
��1����ÿ����ͨӣ����xԪ����ÿ����Ƥӣ������x+20��Ԫ�������ܼ�=������������ϵ��������۶����26000Ԫ�����ɵó�����x��һԪһ�β���ʽ����֮ȡ����Сֵ���ɵó����ۣ�
��2�������ܼ�=�������������5��1�������۶��4��30��������![]() �����ɵó�����a��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
�����ɵó�����a��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
��1����ÿ����ͨӣ����xԪ����ÿ����Ƥӣ����(x+20)Ԫ��
�����⣬�ã�200x+400(x+20)26000��
��ã�x30
����ÿ����ͨӣ��������30Ԫ��
�ʴ�Ϊ��30
��2��������ã�
30(1![]() )��200(1+5a%)+(30+20)��400(1+
)��200(1+5a%)+(30+20)��400(1+![]() )=26000��(1+
)=26000��(1+![]() )��
)��
�������ã�a230a=0��
��ã�a1=0(��ȥ)��a2=30
��a��ֵΪ30
�ʴ�Ϊ��30



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P����������ABC�ڵ�һ�㣬��PA=6��PB=8��PC=10������APB�Ƶ�B��ʱ����תһ���ǶȺɵõ���CQB�� 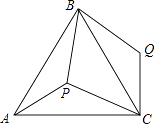
��1�����P���Q֮��ľ��룻
��2�����APB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=4x2��2ax+b��x���ཻ��A��x1 �� 0����B��x2 �� 0����0��x1��x2�����㣬��y�ύ�ڵ�C��
��1����AB=2��tan��ABC=4����������ߵĽ���ʽ��
��2���ڣ�1���У�����DΪֱ��BC�·���������һ���㣬����BCD��������ʱ�����D�����ꣻ
��3���Ƿ��������a��bʹ��1��x1��2��1��x2��2ͬʱ��������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABO�Ķ���A��˫���� ![]() ��ֱ��
��ֱ�� ![]() �ڵڶ����Ľ��㣬AB��
�ڵڶ����Ľ��㣬AB�� ![]() ���ڵ�B��S��ABO=
���ڵ�B��S��ABO= ![]() .
.
��1���������������Ľ���ʽ��
��2����ֱ����˫���ߵ���������A��C�����ꣻ
��3�����AOC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲�����˾һ���ļ����д��������߲�����ȫ�����أ������������߲˲�ֵ�������ӣ�2014���߲˵IJ�ֵ��640��Ԫ��2016���ֵ�ﵽ1000��Ԫ.
��1����2015�ꡢ2016���߲˲�ֵ��ƽ���������Ƕ��٣�
��2����2017���߲˲�ֵ�����ȶ�������������������ǰ���������������ͬ������ô�������2017��ù�˾���߲˲�ֵ�ﵽ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��l��m���ȱߡ�ABC�Ķ���B��ֱ��m�ϣ���BC��ֱ��m�������Ϊ20�㣬��Ϧ��Ķ���Ϊ�� ��
A.60��![]()
B.45��
C.40��
D.30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����������BD��CE�ཻ�ڵ�F����֪��ABC=60�㣬AB=10��CF=EF�����ABC�����Ϊ�� �� 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ƻ��Ӱ칫��Ʒ��˾����A��B�����ͺŵ�С�ڰ壮��Ǣ̸������һ��A��С�ڰ�ȹ���һ��B��С�ڰ����20Ԫ���ҹ���5��A��С�ڰ��4��B��С�ڰ干��820Ԫ��
��1������һ��A��С�ڰ塢һ��B��С�ڰ�������Ԫ��
��2�����ݸ���ѧʵ���������ӹ�˾����A��B�����ͺŵ�С�ڰ干60�飬Ҫ����A��B�����ͺ�С�ڰ���ܷ��ò�����5240Ԫ�����ҹ���A��С�ڰ��������С�ڹ���B��С�ڰ�������![]() �������ѧ�ӹ�˾����A��B�����ͺŵ�С�ڰ����ļ��ַ��������ַ������ܷ�����ͣ�
�������ѧ�ӹ�˾����A��B�����ͺŵ�С�ڰ����ļ��ַ��������ַ������ܷ�����ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AB=AC��M��N�ֱ���AB��AC���е㣬D��EΪBC�ϵĵ㣬����DN��EM����AB=5cm��BC=8cm��DE=4cm����ͼ����Ӱ���ֵ����Ϊ( )
A.1cm2
B.1.5cm2
C.2cm2
D.3cm2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com