
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
【答案】A
【解析】解:连接AF延长AF交BC于G.设EF=CF=x, ∵BD、CE是高,
∴AG⊥BC,
∵∠ABC=60°,∠AGB=90°,
∴∠BAG=30°,
在Rt△AEF中,∵EF=x,∠EAF=30°,∴AE= ![]() x,
x,
在Rt△BCE中,∵EC=2x,∠CBE=60°,∴BE= ![]() x.
x.
∴ ![]() x+
x+ ![]() x=10,
x=10,
∴x=2 ![]() ,
,
∴CE=4 ![]() ,
,
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×10×4
×10×4 ![]() =20
=20 ![]() .
.
故选A.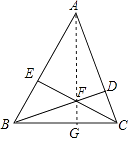
连接AF延长AF交BC于G.设EF=CF=x,连接AF延长AF交BC于G.设EF=CF=x,因为BD、CE是高,所以AG⊥BC,由∠ABC=60°,∠AGB=90°,推出∠BAG=30°,在Rt△AEF中,由EF=x,∠EAF=30°可得AE= ![]() x,在Rt△BCE中,由EC=2x,∠CBE=60°可得BE=
x,在Rt△BCE中,由EC=2x,∠CBE=60°可得BE= ![]() x.可得
x.可得 ![]() x+
x+ ![]() x=10,解方程即可解决问题.
x=10,解方程即可解决问题.


科目:初中数学 来源: 题型:
【题目】把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )
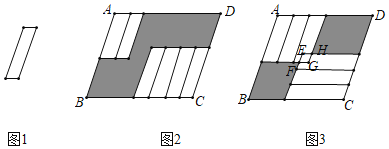
A.0.5B.1C.1.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的解题过程(在下面的横线上,填写相应的结论或推理的依据):
已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
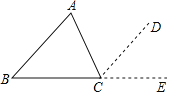
解:∠A+∠B+∠C=180°
理由:过C作CD//AB,并延长BC到E
∵CD//________(已作)
∴∠________=∠ACD(两直线平行,内错角相等)
且∠B=∠___________(________________)
而∠DCE+∠ACD+∠ACB=_________°
∴∠________+∠B+∠ACB=180°(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“四月江南黄鸟肥,樱桃满市粲朝辉”,暮春时节,重庆市樱桃(俗称思桃儿)早已进入采摘期.某现代农业园区推行免入园费自助采摘活动.该园区种植了普通樱桃和乌皮樱桃两个品种,其中乌皮樱桃甜味香,肉质细嫩,售价比普通樱桃每斤高出20元.
(1)今年4月30日,普通樱桃销量为200斤,乌皮樱桃销量为400斤,若当天总销售额不低于26000元,则每斤普通樱桃至少卖多少元?
(2)为降低高温天气带来的经济损失,果园负责人决定在“五一”节推出优惠政策,若两种樱桃在(1)的条件下均以最低价格销售,5月1日,普通樱桃售价降低![]() ,销量比4月30日增加
,销量比4月30日增加![]() ,乌皮樱桃售价不变,销量比4月30日增加了
,乌皮樱桃售价不变,销量比4月30日增加了![]() ,且5月1日总销售额比4月30日增加了
,且5月1日总销售额比4月30日增加了![]() .求
.求![]() 的值.(
的值.(![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1 , L2:y=k2x+b2 , 若L1⊥L2 , 则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y= ![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在函数![]() (x>0)的图象上,点B在直线
(x>0)的图象上,点B在直线![]() (k为常数,且k
(k为常数,且k![]() 0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.只有1对或2对
B.只有1对
C.只有2对
D.只有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段![]() ,动点
,动点![]() 以
以![]() 的速度从
的速度从![]() 在线段
在线段![]() 上运动,到达点
上运动,到达点![]() 后,停止运动;动点
后,停止运动;动点![]() 以
以![]() 的速度从
的速度从![]() 在线段
在线段![]() 上运动,到达点
上运动,到达点![]() 后,停止运动.若动点
后,停止运动.若动点![]() 同时出发,设点
同时出发,设点![]() 的运动时间是
的运动时间是![]() (单位:
(单位:![]() )时,两个动点之间的距离为S(单位:
)时,两个动点之间的距离为S(单位:![]() ),则能表示
),则能表示![]() 与
与![]() 的函数关系的是( )
的函数关系的是( )
![]()
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是四边形ABCD边上的一个动点.
是四边形ABCD边上的一个动点.
(1)若四边形ABCD是菱形,求点![]() 的坐标.
的坐标.
(2)如图1,若![]() ,点
,点![]() 在第四象限内
在第四象限内
①若点![]() 在边
在边![]() ,
,![]() 上,点
上,点![]() 关于坐标轴对称的点
关于坐标轴对称的点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标.
的坐标.
②若点![]() 在边
在边![]() ,
,![]() ,
,![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点,如图2,过点
轴的交点,如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,它们相交于点
,它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com