
【题目】完成下面的解题过程(在下面的横线上,填写相应的结论或推理的依据):
已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
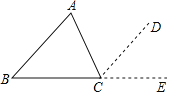
解:∠A+∠B+∠C=180°
理由:过C作CD//AB,并延长BC到E
∵CD//________(已作)
∴∠________=∠ACD(两直线平行,内错角相等)
且∠B=∠___________(________________)
而∠DCE+∠ACD+∠ACB=_________°
∴∠________+∠B+∠ACB=180°(__________)
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民户一表生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 17 吨但不超过 30 吨的部分 |
|
|
超过 30 吨的部分 |
|
|
说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费.
(1)设小王家一个月的用水量为![]() 吨,所应交的水费为
吨,所应交的水费为![]() 元,请写出
元,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把7月份的水费控制在不超过家庭月收入的![]() .若小王家的月收入为
.若小王家的月收入为![]() 元,则小王家7月份最多能用多少吨水?
元,则小王家7月份最多能用多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AE等于弧AB,BE分别交AD、AC于点F、G. 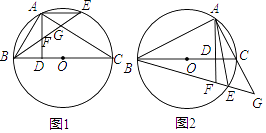
(1)判断△FAG的形状,并说明理由;
(2)若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线 ![]() 过A、B两点.
过A、B两点.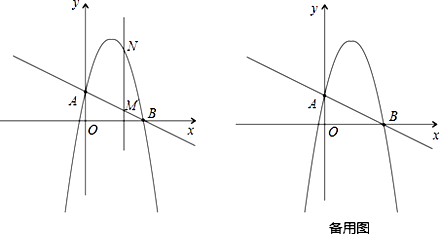
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线 ![]() 与直线
与直线 ![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ ![]() 轴于点B且S△ABO=
轴于点B且S△ABO= ![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜有限公司一年四季都有大量新鲜蔬菜销往全国各地,近年来它的蔬菜产值不断增加,2014年蔬菜的产值是640万元,2016年产值达到1000万元.
(1)求2015年、2016年蔬菜产值的平均增长率是多少?
(2)若2017年蔬菜产值继续稳定增长(即年增长率与前两年的年增长率相同),那么请你估计2017年该公司的蔬菜产值达到多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的是_________.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com