
【题目】在直角三角形△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的是_________.(填序号)

【答案】①②④
【解析】
根据三角形内角和定理以及角平分线的定义即可判断①;根据平行线的性质和已知条件即可判断②;由∠ABC的度数不确定即可判断③;根据余角的性质和角平分线的定义即可判断④,进而可得结论.
解:∵AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,
∴∠BAF=![]() ∠BAC,∠ABF=
∠BAC,∠ABF=![]() ∠ABC,
∠ABC,
∵∠C=90°,
∴∠ABC+∠BAC=90°,
∴∠BAF+∠ABF=45°,
∴∠AFB=135°,故①正确;
∵DG∥AB,
∴∠BDG=∠ABC=2∠CBE,故②正确;
∵∠ABC的度数不确定,
∴BC平分∠ABG不一定成立,故③错误;
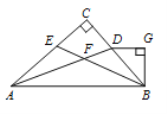
∵BE平分∠ABC,
∴∠ABF=∠CBE,
又∵∠C=∠ABG=90°,
∴∠BEC+∠CBE=90°,∠ABF+∠FBG=90°,
∴∠BEC=∠FBG,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】完成下面的解题过程(在下面的横线上,填写相应的结论或推理的依据):
已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
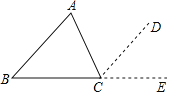
解:∠A+∠B+∠C=180°
理由:过C作CD//AB,并延长BC到E
∵CD//________(已作)
∴∠________=∠ACD(两直线平行,内错角相等)
且∠B=∠___________(________________)
而∠DCE+∠ACD+∠ACB=_________°
∴∠________+∠B+∠ACB=180°(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段![]() ,动点
,动点![]() 以
以![]() 的速度从
的速度从![]() 在线段
在线段![]() 上运动,到达点
上运动,到达点![]() 后,停止运动;动点
后,停止运动;动点![]() 以
以![]() 的速度从
的速度从![]() 在线段
在线段![]() 上运动,到达点
上运动,到达点![]() 后,停止运动.若动点
后,停止运动.若动点![]() 同时出发,设点
同时出发,设点![]() 的运动时间是
的运动时间是![]() (单位:
(单位:![]() )时,两个动点之间的距离为S(单位:
)时,两个动点之间的距离为S(单位:![]() ),则能表示
),则能表示![]() 与
与![]() 的函数关系的是( )
的函数关系的是( )
![]()
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
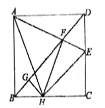
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .在以下四个结论中:①
.在以下四个结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长为12.其中正确的结论有__________(填序号)
的周长为12.其中正确的结论有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
解方程x4﹣7x2+12=0这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,则x4=y2 , ∴原方程可化为:y2﹣7y+12=0,解得y1=3,y2=4,当y=3时,x2=3,x=± ![]() ,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1=
,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1= ![]() ,x2=﹣
,x2=﹣ ![]() ,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:(x2+x)2﹣5(x2+x)+4=0;
(2)已知实数a,b满足(a2+b2)2﹣3(a2+b2)﹣10=0,试求a2+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
对于任意一个三位数正整数n,如果n的各个数位上的数字互不相同,且都不为零,那么称这个数为“陌生数”,将一个“陌生数”的三个数位上的数字交换顺序,可以得到5个不同的新“陌生数”,把这6个陌生数的和与111的商记为M(n).例如n=123,可以得到132.213.231.312.321这5个新的“陌生数”,这6个“陌生数”的和为123+132+213+231+312+321=1332,因为![]() ,所以M(123)=12.
,所以M(123)=12.
(1)计算:M(125)和M(361)的值;
(2)设s和t都是“陌生数”,其中4和2分别是s的十位和个位上的数字,2和5分别是t的百位和个位上的数字,且t的十位上的数字比s的百位上的数字小2;规定:![]() .若
.若![]() ,则k的值是多少?
,则k的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是四边形ABCD边上的一个动点.
是四边形ABCD边上的一个动点.
(1)若四边形ABCD是菱形,求点![]() 的坐标.
的坐标.
(2)如图1,若![]() ,点
,点![]() 在第四象限内
在第四象限内
①若点![]() 在边
在边![]() ,
,![]() 上,点
上,点![]() 关于坐标轴对称的点
关于坐标轴对称的点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标.
的坐标.
②若点![]() 在边
在边![]() ,
,![]() ,
,![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点,如图2,过点
轴的交点,如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,它们相交于点
,它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是等边三角形
都是等边三角形

(1)求证:四边形![]() 是菱形
是菱形
(2)给![]() 方向将
方向将![]() 平移到
平移到![]() 的位置如图2,此时,四边形
的位置如图2,此时,四边形![]() (如图3)是平行四边形吗?
(如图3)是平行四边形吗?
(3)若按(2)题的方式继续平移![]() 到
到![]() ,当在什么位置时,四边形
,当在什么位置时,四边形![]() 是矩形,请画出
是矩形,请画出![]() 的位置(如图4),并证明你的结论
的位置(如图4),并证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com