
【题目】已知四边形ABCD,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是四边形ABCD边上的一个动点.
是四边形ABCD边上的一个动点.
(1)若四边形ABCD是菱形,求点![]() 的坐标.
的坐标.
(2)如图1,若![]() ,点
,点![]() 在第四象限内
在第四象限内
①若点![]() 在边
在边![]() ,
,![]() 上,点
上,点![]() 关于坐标轴对称的点
关于坐标轴对称的点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标.
的坐标.
②若点![]() 在边
在边![]() ,
,![]() ,
,![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点,如图2,过点
轴的交点,如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,它们相交于点
,它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)


【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() 或
或![]() 或
或![]() ,②
,②![]() 或
或![]() 或
或 或
或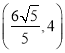
【解析】
(1)由![]() 轴,得点
轴,得点![]() 的纵坐标为-4,再求AD的长,即可求出点
的纵坐标为-4,再求AD的长,即可求出点![]() 的坐标
的坐标
;
(2) ①分两种情况讨论,当点![]() 在边
在边![]() 上时和当点
上时和当点![]() 在边
在边![]() 上时,分别求解即可;
上时,分别求解即可;
②分三种情况讨论,当点![]() 在线段
在线段![]() 上时,当点
上时,当点![]() 在
在![]() 上时,当点
上时,当点![]() 在线段
在线段![]() 上时,分别求解即可.
上时,分别求解即可.
解:(1)∵![]() 轴,
轴,
∴点![]() 的纵坐标为-4,
的纵坐标为-4,
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴AD=![]() =
= ![]() ,
,
∴点![]() 的横坐标为1+
的横坐标为1+![]() ,
,
点![]() 的坐标为
的坐标为![]() ;
;
(2)①当点![]() 在边
在边![]() 上时,
上时,
∵直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,且
,且![]() ,
,
若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
解得![]() ,
,
此时![]() .
.
若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上时,
上时,
∴![]() ,解得
,解得![]() ,此时
,此时![]()
②当点![]() 在边
在边![]() 上时,设
上时,设![]() 且
且![]() ,
,
若等![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
∴![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
解得![]() .此时
.此时![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
(3)①如图1中,

当点![]() 在线段
在线段![]() 上时,设
上时,设![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]()
∴![]() ,
,
解得![]() ,
,
∴
根据对称性可知,![]() 也满足条件.
也满足条件.
②如图2中,

当点![]() 在
在![]() 上时,易知四边形
上时,易知四边形![]() 是正方形,边长为2,此时
是正方形,边长为2,此时![]() .
.
③如图3中,

当点![]() 在线段
在线段![]() 上时,设
上时,设![]() 交
交![]() 轴于
轴于![]() .易证
.易证![]() ,推出
,推出![]() ,设
,设![]() .
.
∵直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
在![]() 中,有
中,有![]() ,解得
,解得![]() ,
,
∴![]() .
.
点![]() 坐标为
坐标为![]() 或
或![]() 或
或 或
或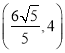 .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的是_________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=5cm,BC=8cm,DE=4cm,则图中阴影部分的面积为( )
A.1cm2
B.1.5cm2
C.2cm2
D.3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是.
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种泰山旅游纪念品,4月的营业额为2000元,为扩大销售量,5月份该商店对这种纪念品打9折销售,结果销售量增加20件,营业额增加700元.
(1)求该种纪念品4月份的销售价格;
(2)若4月份销售这种纪念品获利800元,5月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,![]() 级:对学习很感兴趣;
级:对学习很感兴趣;![]() 级:对学习较感兴趣;
级:对学习较感兴趣;![]() 级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:

(1)此次抽样调查中,共调查了多少名学生;
(2)将图①补充完整;
(3)求出图②中![]() 级所占的圆心角的度数;
级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该县近12000名八年级学生中大约有多少名学生学习态度达标(达标包括![]() 级和
级和![]() 级)?
级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3
(2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)(2a+1)2﹣(2a+1)(2a﹣1)
(4)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com