
【题目】如图,Rt△ABO的顶点A是双曲线 ![]() 与直线
与直线 ![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ ![]() 轴于点B且S△ABO=
轴于点B且S△ABO= ![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积.
【答案】
(1)解:如图所示:
设A点坐标为(x,y),且x<0,y>0
则S△ABO= ![]() |OB||AB|=
|OB||AB|= ![]() (﹣x)y=
(﹣x)y= ![]()
∴xy=﹣3
又∵y= ![]() ∴k=﹣3
∴k=﹣3
∴所求的两个函数的解析式分别为y=﹣ ![]() ,y=﹣x +2
,y=﹣x +2
(2)解:A、C两点坐标满足
解得 ![]()
∴交点A为(﹣1,3),C为(3,﹣1)
(3)解:由y=﹣x+2,令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2)![]()
【解析】(1)抓住已知条件,点A是两函数图像在第二象限的交点,因此设点A的坐标为(x,y),根据△ABO的面积是![]() |xy|=
|xy|=![]() ,求出xy的值,即可得出k的值。
,求出xy的值,即可得出k的值。
(2)将两函数解析式联立方程组,求出方程组的解,即可得出交点A、C的坐标。
(3)先求出直线y=﹣x+2与y轴的交点D的坐标,再根据S△ACO=S△ADO+S△CDO , 计算即可求出答案。
【考点精析】利用确定一次函数的表达式和三角形的面积对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),沿
重合),沿![]() 折叠该纸片,点
折叠该纸片,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() .
.

(1)如图1,当点![]() 在第一象限,且
在第一象限,且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当点![]() 为
为![]() 的中点时;
的中点时;
①求证:![]() ;
;
②直接写出四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△ ![]() 的位置,点B,O分别落在点
的位置,点B,O分别落在点 ![]() ,
, ![]() 处,点
处,点 ![]() 在
在 ![]() 轴上,再将△
轴上,再将△ ![]() 绕点
绕点 ![]() 顺时针旋转到△
顺时针旋转到△ ![]() 的位置,点
的位置,点 ![]() 在
在 ![]() 轴上,将△
轴上,将△ ![]() 绕点
绕点 ![]() 顺时针旋转△
顺时针旋转△ ![]() 的位置,点
的位置,点 ![]() 在
在 ![]() 轴上……依次进行下去。若点
轴上……依次进行下去。若点 ![]() ,B(0,2),则点
,B(0,2),则点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的解题过程(在下面的横线上,填写相应的结论或推理的依据):
已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
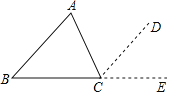
解:∠A+∠B+∠C=180°
理由:过C作CD//AB,并延长BC到E
∵CD//________(已作)
∴∠________=∠ACD(两直线平行,内错角相等)
且∠B=∠___________(________________)
而∠DCE+∠ACD+∠ACB=_________°
∴∠________+∠B+∠ACB=180°(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段平直的公路上有![]() 三个城市,
三个城市,![]() 城在
城在![]() 城和
城和![]() 城之间,一辆慢车从
城之间,一辆慢车从![]() 城出发匀速开往
城出发匀速开往![]() 城,与此同时一辆快车从
城,与此同时一辆快车从![]() 城出发匀速开往
城出发匀速开往![]() 城.当慢车到达
城.当慢车到达![]() 城后立即以
城后立即以![]() 倍原速匀速返回到
倍原速匀速返回到![]() 城.当快车到达
城.当快车到达![]() 城后,休息了半小时后再提高原速的
城后,休息了半小时后再提高原速的![]() 的速度匀速开往
的速度匀速开往![]() 城.下图是慢车出发后的时间
城.下图是慢车出发后的时间![]() (小时)与两车之间的距离
(小时)与两车之间的距离![]() (千米)之间的函数关系图,慢车出发6小时后,两车相距___________千米.
(千米)之间的函数关系图,慢车出发6小时后,两车相距___________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“四月江南黄鸟肥,樱桃满市粲朝辉”,暮春时节,重庆市樱桃(俗称思桃儿)早已进入采摘期.某现代农业园区推行免入园费自助采摘活动.该园区种植了普通樱桃和乌皮樱桃两个品种,其中乌皮樱桃甜味香,肉质细嫩,售价比普通樱桃每斤高出20元.
(1)今年4月30日,普通樱桃销量为200斤,乌皮樱桃销量为400斤,若当天总销售额不低于26000元,则每斤普通樱桃至少卖多少元?
(2)为降低高温天气带来的经济损失,果园负责人决定在“五一”节推出优惠政策,若两种樱桃在(1)的条件下均以最低价格销售,5月1日,普通樱桃售价降低![]() ,销量比4月30日增加
,销量比4月30日增加![]() ,乌皮樱桃售价不变,销量比4月30日增加了
,乌皮樱桃售价不变,销量比4月30日增加了![]() ,且5月1日总销售额比4月30日增加了
,且5月1日总销售额比4月30日增加了![]() .求
.求![]() 的值.(
的值.(![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在函数![]() (x>0)的图象上,点B在直线
(x>0)的图象上,点B在直线![]() (k为常数,且k
(k为常数,且k![]() 0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
0)上,若A,B两点关于原点对称,则称点A,B为函数y1 , y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.只有1对或2对
B.只有1对
C.只有2对
D.只有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
解方程x4﹣7x2+12=0这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,则x4=y2 , ∴原方程可化为:y2﹣7y+12=0,解得y1=3,y2=4,当y=3时,x2=3,x=± ![]() ,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1=
,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1= ![]() ,x2=﹣
,x2=﹣ ![]() ,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:(x2+x)2﹣5(x2+x)+4=0;
(2)已知实数a,b满足(a2+b2)2﹣3(a2+b2)﹣10=0,试求a2+b2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com