练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一段平直的公路上有三个城市，城在城和城之间，一辆慢车从城出发匀速开往城，与此同时一辆快车从城出发匀速开往城．当慢车到达城后立即以倍原速匀速返回到城．当快车到达城后，休息了半小时后再提高原速的的速度匀速开往城．下图是慢车出发后的时间（小时）与两车之间的距离（千米）之间的函数关系图，慢车出发6小时后，两车相距___________千米．

    【答案】25

    【解析】

    由图可知A，B两地的距离为240千米；快车从B城出发匀速开往C城用了2小时，两车的距离增加了80千米，故快车原速比慢车原速快40千米/时；慢车用了4小时到达B地，据此可以求出慢车原速与快车原速，进而求出B，C两地的距离，然后根据“路程=时间×速度”解答即可．

    由题意可知A，B两地的距离为240千米；慢车用了4小时到达B地；

    故慢车原速为：240÷4=60千米/时；

    ∴快车原速为：60+(320240)÷2=100千米/时；

    B，C两地的距离为：100×2=200千米，

    ∴慢车出发6小时后，两车相距为：

    (620.5)×100×(1+10%)200(64)×60×=25千米

    故答案为：25

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

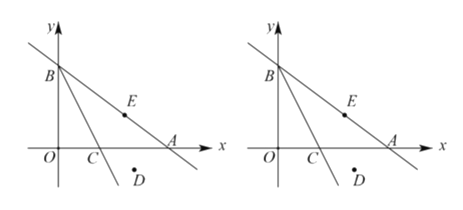
    【题目】已知直线与轴，轴分别交于点，将对折，使点的对称点落在直线上，折痕交轴于点．

    （1）求点的坐标；

    （2）若已知第四象限内的点，在直线上是否存在点，使得四边形为平行四边形？若存在，求出点的坐标；若不存在，说明理由；

    （3）设经过点且与轴垂直的直线与直线的交点为为线段上一点，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将线段AB绕点A逆时针旋转60°得AC，连接BC，作△ABC的外接圆⊙O，点P为劣弧 上的一个动点，弦AB，CP相交于点D．

    （1）求∠APB的大小；
    （2）当点P运动到何处时，PD⊥AB？并求此时CD：CP的值；
    （3）在点P运动过程中，比较PC与AP+PB的大小关系，并对结论给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，AB//EG//x轴，BC//DE//HG//AP//y轴，点D、C、P、H在x轴上，A(1，2)，B(-1，2)，D(-3，0)，E(-3，-2)，G(3，-2)，把一条长为2019个单位长度且没有弹性的细线（粗细忽略不计）的一端固定在点A处，并按A-B-C-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是（ ）

    A.(1，2)B.(-1，2)C.(-1，-2)D.(1，1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABO的顶点A是双曲线 与直线 在第二象限的交点，AB⊥ 轴于点B且S△ABO= .

    （1）求这两个函数的解析式；
    （2）求直线与双曲线的两个交点A，C的坐标；
    （3）求△AOC的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年5月12日是我国第11个全国防灾减灾日，重庆某中学为普及推广全民防灾减灾知识和避灾自救技能，开展了“提高灾害防治能力，构筑生命安全防线”知识竞赛活动．初一、初二年级各500人，为了调查竞赛情况，学校进行了抽样调查，过程如下，请根据表格回答问题．

    收集数据：

    从初一、初二年级各抽取20名同学的测试成绩（单位：分），记录如下：

    初一：68、79、100、98、98、86、88、99、100、93、90、100、80、76、84、98、99、86、98、90

    初二：92、89、100、99、98、94、100、62、100、86、75、98、89、100、100、68、79、100、92、89

    整理数据：

    表一

    分数段

    初一人数

    1

    12

    初二人数

    2

    2

    4

    12

    分析数据：

    表二

    种类

    平均数

    中位数

    众数

    方差

    初一

    90.5

    91.5

    84.75

    初二

    90.5

    100

    123.05

    得出结论：

    （1）在表中：_______，_______，_______，_______；

    （2）得分情况较稳定的是___________（填初一或初二）；

    （3）估计该校初一、初二年级学生本次测试成绩中可以得满分的人数共有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，l∥m，等边△ABC的顶点B在直线m上，边BC与直线m所夹锐角为20°，则∠α的度数为（ ）

    A.60°
    B.45°
    C.40°
    D.30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以Rt△ABC的斜边BC为边，在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO．若AB＝4，AO＝6，则AC的长等于（　　）

    A. 12B. 16C. 8+6D. 4+6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某数学兴趣小组开展了一次活动，过程如下：如图1，等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将三角板中含45°角的顶点放在A上，斜边从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．

    （1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；
    （2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2 ． 同组的小颖和小亮随后想出了两种不同的方法进行解决：
    小颖的想法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）；
    小亮的想法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）；
    请你从中任选一种方法进行证明．
    （3）小敏继续旋转三角板，请你继续研究：当135°＜α＜180°时（如图4），等量BD2+CE2=DE2是否仍然成立？请作出判断，不需要证明．

    查看答案和解析>>

    同步练习册答案