
【题目】如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧 ![]() 上的一个动点,弦AB,CP相交于点D.
上的一个动点,弦AB,CP相交于点D. 
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
【答案】
(1)解:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵∠APB+∠ACB=180°,
∴∠APB=120°
(2)解:当点P运动到 ![]() 的中点时,PD⊥AB,
的中点时,PD⊥AB,
如图1,连接PC,OA,OB,设⊙O的半径为r,则CP=2r,
又∵⊙O为等边△ABC的外接圆,
∴∠OAB=30°,
在Rt△OAD中,
∵OD= ![]() OA=
OA= ![]() ,
,
∴CD= ![]() +r=
+r= ![]() ,
,
∴CD:CP= ![]() :2r=3:4
:2r=3:4
(3)解:PC=AP+PB
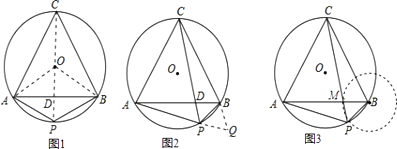
证明:方法一:
如图2,在AP的延长线上取点Q,使PQ=PB,连接BQ,
∵∠APB=120°,
∴∠BPQ=60°,
∴△BPQ是等边三角形,
∴PB=BQ,
∵∠CBP=∠CBA+∠ABP=60°+∠ABP,
∠ABQ=∠QBP+∠ABP=60°+∠ABP,
∴∠ABQ=∠CBP,
在△ABQ和△CBP中,PB=QB,∠CBP=∠ABQ,CB=AB,
∴△ABQ≌△CBP,
∴CP=AQ=AP+PQ=AP+PB,即PC=AP+PB;
方法二:如图3,B为圆心,BP为半径画圆交CP于点M,连接BM,
∵∠CPB=60°,
∴△PBM是等边三角形,
∵∠CMB=120°,
∴∠CMB=∠APB,
∴△APB≌△CMB,
∴PC=AP+PB;
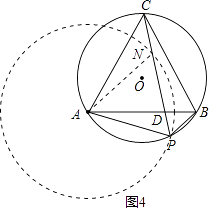
方法三:(略证)如图4,以A为圆心,A为半径画圆交CP于N,连接AN,
先证△APN是等边三角形,再证△ANC≌△APB,
从而PC=AP+PB.
【解析】(1)先根据题意判断出△ABC是等边三角形,再根据圆内接四边形对角互补的性质可知∠APB+∠ACB=180°,进而可得出结论;(2)连接PC,OA,OB,设⊙O的半径为r,则CP=2r,根据⊙O为等边△ABC的外接圆可求出∠OAB=30°,再根据直角三角形的性质可用r表示出OD,CD的值,进而得出结论;(3)在AP的延长线上取点Q,使PQ=PB,连接BQ,可判断出△BPQ是等边三角形,再根据全等三角形的判定定理得出△ABQ≌△CBP,由全等三角形的性质即可得出结论.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整
如图,已知AD⊥BC于D,点E在BA的延长线上,EG⊥BC于C,交AC于点F,∠E=∠1.求证:AD平分∠BAC.

证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=∠EGC=90°( ),
∴AD∥EG( ),
∴∠1=∠2( ),
∴_____=∠3( ),
又∵∠E=∠1(已知),∴∠2=∠3( ),
∴AD平分∠BAC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(x,y),点B(x﹣my,mx﹣y)(其中m为常数,且m≠0),则称B是点A的“m族衍生点”.例如:点A(1,2)的“3族衍生点”B的坐标为(1﹣3×2,3×1﹣2),即B(﹣5,1).
(1)点(2,0)的“2族衍生点”的坐标为 ;
(2)若点A的“3族衍生点”B的坐标是(﹣1,5),则点A的坐标为 ;
(3)若点A(x,0)(其中x≠0),点A的“m族衍生点“为点B,且AB=OA,求m的值;
(4)若点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,则点A的位置在 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某商场搞优惠促销活动,其活动内容是:“凡在本商场一次性购物超过100元者,超过100元的部分按9折优惠”.在此活动中,李明到该商场为单位一次性购买单价为60元的办公用品x(x>2)件,则应付款y(元)与商品件数x(件)之间的关系式是( )
A.y=54xB.y=54x+10
C.y=54x-90D.y=54x+45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),沿
重合),沿![]() 折叠该纸片,点
折叠该纸片,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() .
.

(1)如图1,当点![]() 在第一象限,且
在第一象限,且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当点![]() 为
为![]() 的中点时;
的中点时;
①求证:![]() ;
;
②直接写出四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△ ![]() 的位置,点B,O分别落在点
的位置,点B,O分别落在点 ![]() ,
, ![]() 处,点
处,点 ![]() 在
在 ![]() 轴上,再将△
轴上,再将△ ![]() 绕点
绕点 ![]() 顺时针旋转到△
顺时针旋转到△ ![]() 的位置,点
的位置,点 ![]() 在
在 ![]() 轴上,将△
轴上,将△ ![]() 绕点
绕点 ![]() 顺时针旋转△
顺时针旋转△ ![]() 的位置,点
的位置,点 ![]() 在
在 ![]() 轴上……依次进行下去。若点
轴上……依次进行下去。若点 ![]() ,B(0,2),则点
,B(0,2),则点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段平直的公路上有![]() 三个城市,
三个城市,![]() 城在
城在![]() 城和
城和![]() 城之间,一辆慢车从
城之间,一辆慢车从![]() 城出发匀速开往
城出发匀速开往![]() 城,与此同时一辆快车从
城,与此同时一辆快车从![]() 城出发匀速开往
城出发匀速开往![]() 城.当慢车到达
城.当慢车到达![]() 城后立即以
城后立即以![]() 倍原速匀速返回到
倍原速匀速返回到![]() 城.当快车到达
城.当快车到达![]() 城后,休息了半小时后再提高原速的
城后,休息了半小时后再提高原速的![]() 的速度匀速开往
的速度匀速开往![]() 城.下图是慢车出发后的时间
城.下图是慢车出发后的时间![]() (小时)与两车之间的距离
(小时)与两车之间的距离![]() (千米)之间的函数关系图,慢车出发6小时后,两车相距___________千米.
(千米)之间的函数关系图,慢车出发6小时后,两车相距___________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 O 是边 AC 上一个动点,过 O 作直线 MN∥BC,设 MN 交∠ACB 的平分线于点 E,交∠ACB 的外角平分线于点 F.
(1)求证:OE=OF;
(2)当点 O 在边 AC 上运动到什么位置时,四边形 AECF 是矩形?并说明理由.
(3)若 AC 边上存在点 O,使四边形 AECF 是正方形,猜想△ABC 的形状并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com