
【题目】某数学兴趣小组开展了一次活动,过程如下:如图1,等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将三角板中含45°角的顶点放在A上,斜边从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2 . 同组的小颖和小亮随后想出了两种不同的方法进行解决:
小颖的想法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2);
小亮的想法:将△ABD绕点A逆时针旋转90°得到△ACG,连接EG(如图3);
请你从中任选一种方法进行证明.
(3)小敏继续旋转三角板,请你继续研究:当135°<α<180°时(如图4),等量BD2+CE2=DE2是否仍然成立?请作出判断,不需要证明.
【答案】
(1)证明:如图1,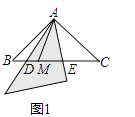
∵∠BAC=90°,
∴∠BAD+∠DAM+∠MAE+∠EAC=90°.
∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∵∠BAD=∠DAM,
∴∠BAD+∠EAC=∠DAM+∠EAC=45°,
∴∠BAD+∠MAE=∠DAM+∠EAC,
∴∠MAE=∠EAC,即AE平分∠MAC
(2)解:选择小颖的方法.
证明:如图2,连接EF.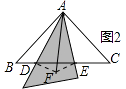
由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
∴由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,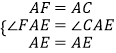
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2 ,
∴BD2+CE2=DE2 .
选择小亮的方法,
证明:∵将△ABD绕点A逆时针旋转90°得到△ACG,
∴△ADB≌△AGC,
∴∠B=∠ACG=45°,AD=AG,BD=CG,
∵∠BAC=∠DAG=90°,∠DAE=45°,
∴∠EAG=45°,
在△DAE和△GAE中,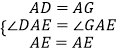 ,
,
∴△DAE≌△GAE(SAS),
∴DE=EG,
∵∠ACB=90°,
∴∠ECG=∠ACB+∠ACG=45°+45°=90°,
∴△ECG是直角三角形,
∴CG2+CE2=EG2 ,
即BD2+CE2=DE2
(3)解:当135°<α<180°时,等量关系BD2+CE2=DE2仍然成立.证明如下:
如图4,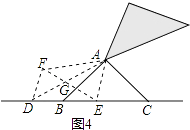
按小颖的方法作图,设AB与EF相交于点G.
∵将△ABD沿AD所在的直线对折得到△ADF,
∴AF=AB,∠AFD=∠ABD=135°,∠BAD=∠FAD.
又∵AC=AB,∴AF=AC.
又∵∠CAE=90°﹣∠BAE=90°﹣(45°﹣∠BAD)=45°+∠BAD=45°+∠FAD=∠FAE.
∴∠CAE=∠FAE.
在△AEF和△AEC中,
∵ 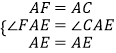 ,
,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD﹣∠AFE=∠135°﹣∠C=135°﹣45°=90°.
∴∠DFE=90°.
在Rt△DFE中,DF2+FE2=DE2 ,
∴BD2+CE2=DE2
【解析】(1)利用等式的基本性质和角平分线定义即可证出;(2)利用折叠或旋转,可将BD、CE、DE组合到一个三角形中,利用全等证明得到对应边相等,对应角相等,证出直角三角形,利用勾股定理得到结论;(3)借鉴(2)的思路方法,利用折叠的性质,可得到全等三角形,再利用其性质得到直角三角形,进而得到结论.
【考点精析】利用全等三角形的性质和轴对称的性质对题目进行判断即可得到答案,需要熟知全等三角形的对应边相等; 全等三角形的对应角相等;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】一段平直的公路上有![]() 三个城市,
三个城市,![]() 城在
城在![]() 城和
城和![]() 城之间,一辆慢车从
城之间,一辆慢车从![]() 城出发匀速开往
城出发匀速开往![]() 城,与此同时一辆快车从
城,与此同时一辆快车从![]() 城出发匀速开往
城出发匀速开往![]() 城.当慢车到达
城.当慢车到达![]() 城后立即以
城后立即以![]() 倍原速匀速返回到
倍原速匀速返回到![]() 城.当快车到达
城.当快车到达![]() 城后,休息了半小时后再提高原速的
城后,休息了半小时后再提高原速的![]() 的速度匀速开往
的速度匀速开往![]() 城.下图是慢车出发后的时间
城.下图是慢车出发后的时间![]() (小时)与两车之间的距离
(小时)与两车之间的距离![]() (千米)之间的函数关系图,慢车出发6小时后,两车相距___________千米.
(千米)之间的函数关系图,慢车出发6小时后,两车相距___________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 O 是边 AC 上一个动点,过 O 作直线 MN∥BC,设 MN 交∠ACB 的平分线于点 E,交∠ACB 的外角平分线于点 F.
(1)求证:OE=OF;
(2)当点 O 在边 AC 上运动到什么位置时,四边形 AECF 是矩形?并说明理由.
(3)若 AC 边上存在点 O,使四边形 AECF 是正方形,猜想△ABC 的形状并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,∠ACF= ;
(2)在图1中,若∠BCE=α,∠ACF= (用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,若∠BCE=150°,试求∠ACF与∠ACE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
解方程x4﹣7x2+12=0这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,则x4=y2 , ∴原方程可化为:y2﹣7y+12=0,解得y1=3,y2=4,当y=3时,x2=3,x=± ![]() ,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1=
,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1= ![]() ,x2=﹣
,x2=﹣ ![]() ,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:(x2+x)2﹣5(x2+x)+4=0;
(2)已知实数a,b满足(a2+b2)2﹣3(a2+b2)﹣10=0,试求a2+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新药,在做药效试验时发现,如果成人按规定剂量服用,那么服药后,每毫升血液中含药量y(μg)随时间t(h)的变化图象如图所示,根据图象回答:
(1)服药后几时血液中含药量最高?每毫升血液中含多少微克?
(2)在服药几时内,每毫升血液中含药量逐渐升高?在服药几时后,每毫升血液中含药量逐渐下降?
(3)服药后14 h时,每毫升血液中含药量是多少微克?
(4)如果每毫升血液中含药量为4微克及以上时,治疗疾病有效,那么有效时间为几时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一张菱形纸片ABCD,AC=8,BD=6.
请沿着AC剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图2中用实线画出你所拼成的平行四边形;若沿着BD剪开,请在图3中用实线画出拼成的平行四边形.并直接写出这两个平行四边形的周长.
沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4中用实线画出拼成的平行四边形.(注:上述所画的平行四边形都不能与原菱形全等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
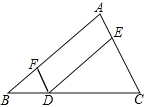
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( ) 
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com