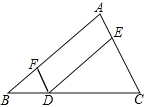
[题目]完成下面的证明.如图点D.E.F分别是三角形ABC的边BC.CA.AB上的点.DE∥BA.DF∥CA．求证:∠FDE＝∠A．证明:∵DE∥AB.∴∠FDE＝∠ ( )∵DF∥CA.∴∠A＝∠ ( )∴∠FDE＝∠A( ) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】完成下面的证明，如图点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE＝∠A．

证明：∵DE∥AB，

∴∠FDE＝∠　　（　　）

∵DF∥CA，

∴∠A＝∠　　（　　）

∴∠FDE＝∠A（　　）

【答案】BFD，两直线平行，内错角相等，BFD，两直线平行，同位角相等，等量代换

【解析】

根据平行线的性质得出∠FDE=∠BFD，∠A=∠BFD，推出即可；

解：证明：∵DE∥AB，

∴∠FDE＝∠BFD（两直线平行，内错角相等）

∵DF∥CA，

∴∠A＝∠BFD（两直线平行，同位角相等）

∴∠FDE＝∠A（等量代换）．

故答案为：BFD，两直线平行，内错角相等，BFD，两直线平行，同位角相等，等量代换．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，以Rt△ABC的斜边BC为边，在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO．若AB＝4，AO＝6，则AC的长等于（　　）

A. 12B. 16C. 8+6D. 4+6

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某数学兴趣小组开展了一次活动，过程如下：如图1，等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将三角板中含45°角的顶点放在A上，斜边从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．

（1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；
（2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2 ．同组的小颖和小亮随后想出了两种不同的方法进行解决：
小颖的想法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）；
小亮的想法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）；
请你从中任选一种方法进行证明．
（3）小敏继续旋转三角板，请你继续研究：当135°＜α＜180°时（如图4），等量BD2+CE2=DE2是否仍然成立？请作出判断，不需要证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）如图甲，，与的关系是什么？并写出推理过程；

（2）如图乙，，直接写出与的数量关系_______________________；

（3）如图丙，，直接写出与的数量关系_____________________．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某商店经销一种泰山旅游纪念品，4月的营业额为2000元，为扩大销售量，5月份该商店对这种纪念品打9折销售，结果销售量增加20件，营业额增加700元.
（1）求该种纪念品4月份的销售价格；
（2）若4月份销售这种纪念品获利800元，5月份销售这种纪念品获利多少元?

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在直角梯形ABCD中，AD∥BC，，AD=6，BC=8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒(t＞0)．

（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．
（2）当BP=1时，求△EPQ与梯形ABCD重叠部分的面积．
（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．