
【题目】(1)如图甲,![]() ,
,![]() 与
与![]() 的关系是什么?并写出推理过程;
的关系是什么?并写出推理过程;
(2)如图乙,![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系_______________________;
的数量关系_______________________;
(3)如图丙,![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系_____________________.
的数量关系_____________________.

【答案】(1)∠BEC=∠1+∠3,理由见解析;(2)∠2+∠4=∠1+∠3+∠5;(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7
【解析】
(1)过点E作EF∥AB,如图甲,根据平行公理的推论可得AB∥CD∥EF,然后根据平行线的性质和角的和差可得结论;
(2)分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,如图乙,根据平行公理的推论可得AB∥CD∥EF∥GH∥MN,然后根据平行线的性质和角的和差可得结论;
(3)分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,如图丙,根据平行公理的推论可得AB∥CD∥EF∥GH∥MN∥KL∥PQ,然后利用平行线的性质和角的和差可得结论.
解:(1)∠BEC=∠1+∠3.
理由如下:过点E作EF∥AB,如图甲,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠BEC=∠BEF+∠CEF=∠1+∠3;
(2)分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,如图乙,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
故答案为:∠2+∠4=∠1+∠3+∠5;
(3)分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,如图丙,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6
=∠BEF+∠FEG+∠GMN+∠KMN+∠KPQ+∠QPC
=∠1+∠EGH+∠HGM+∠LKM+∠LKP+∠7
=∠1+∠3+∠5+∠7.
故答案为:∠2+∠4+∠6=∠1+∠3+∠5+∠7.



科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为边作矩形
为边作矩形![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)求直线![]() 的解析式及
的解析式及![]() 点的坐标.
点的坐标.
(2)如图2,![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 点,
点,![]() 点为直线
点为直线![]() 上两动点(
上两动点(![]() 在上,
在上,![]() 在下),满足
在下),满足![]() ,当
,当![]() 最大时,求
最大时,求![]() 的最小值,并求出此时
的最小值,并求出此时![]() 点的坐标.
点的坐标.
(3)如图3,将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,记旋转后的三角形为
,记旋转后的三角形为![]() ,线段
,线段![]() 所在的直线交直线
所在的直线交直线![]() 于点
于点![]() (
(![]() 不与
不与![]() 、
、![]() 重合),交
重合),交![]() 轴于点
轴于点![]() ,在平面内是否存在一点
,在平面内是否存在一点![]() ,使得以
,使得以![]() 四点形成的四边形为菱形,若存在,请直接写出
四点形成的四边形为菱形,若存在,请直接写出![]() 点的坐标;若不存在,请说出理由.
点的坐标;若不存在,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,∠ACF= ;
(2)在图1中,若∠BCE=α,∠ACF= (用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,若∠BCE=150°,试求∠ACF与∠ACE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新药,在做药效试验时发现,如果成人按规定剂量服用,那么服药后,每毫升血液中含药量y(μg)随时间t(h)的变化图象如图所示,根据图象回答:
(1)服药后几时血液中含药量最高?每毫升血液中含多少微克?
(2)在服药几时内,每毫升血液中含药量逐渐升高?在服药几时后,每毫升血液中含药量逐渐下降?
(3)服药后14 h时,每毫升血液中含药量是多少微克?
(4)如果每毫升血液中含药量为4微克及以上时,治疗疾病有效,那么有效时间为几时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一张菱形纸片ABCD,AC=8,BD=6.
请沿着AC剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图2中用实线画出你所拼成的平行四边形;若沿着BD剪开,请在图3中用实线画出拼成的平行四边形.并直接写出这两个平行四边形的周长.
沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4中用实线画出拼成的平行四边形.(注:上述所画的平行四边形都不能与原菱形全等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2009年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:请根据以上信息解答下列问题
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2009年南县全县农民冬种油菜的总获利多少元?(结果用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
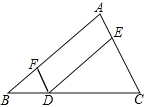
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com