
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ��
��![]() ���ֱ���
���ֱ���![]() ��
��![]() ��������
Ϊ��������![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��
��

��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ������꣮
������꣮
��2����ͼ2��![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣬
��һ���㣬![]() �㣬
�㣬![]() ��Ϊֱ��
��Ϊֱ��![]() �������㣨
�������㣨![]() ���ϣ�
���ϣ�![]() ���£�������
���£�������![]() ����
����![]() ���ʱ����
���ʱ����![]() ����Сֵ���������ʱ
����Сֵ���������ʱ![]() ������꣮
������꣮
��3����ͼ3����![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() ������ת���������Ϊ
������ת���������Ϊ![]() ���߶�
���߶�![]() ���ڵ�ֱ�߽�ֱ��
���ڵ�ֱ�߽�ֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ��
��![]() �غϣ�����
�غϣ�����![]() ���ڵ�
���ڵ�![]() ����ƽ�����Ƿ����һ��
����ƽ�����Ƿ����һ��![]() ��ʹ����
��ʹ����![]() �ĵ��γɵ��ı���Ϊ���Σ������ڣ���ֱ��д��
�ĵ��γɵ��ı���Ϊ���Σ������ڣ���ֱ��д��![]() ������ꣻ�������ڣ���˵�����ɣ�
������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ��H(
��H(![]() ,
,![]() )����2��
)����2��![]() ����3�����ڣ�Q(
����3�����ڣ�Q(![]() ,
,![]() )
)
��������
��1����ͼ1�У���HK��OA��K�����A��C�������꣬���ô���ϵ�������ֱ��AC�Ľ���ʽ����ֱ�����������HK��KO���������H�����꣮
��2��������|PC-PB|��BC���Ƴ�����P��CB���ӳ�����ʱ��|PC-PB|��ֵ���ʱP����3��![]() ������P��G��AC��ʹ��P��G=EF=
������P��G��AC��ʹ��P��G=EF=![]() ����ʱ
����ʱ![]() ����G����ֱ��AC�ĶԳƵ�M������DM��AC��E��GM��AC��
����G����ֱ��AC�ĶԳƵ�M������DM��AC��E��GM��AC��![]() ����ʱP��F+EF+DE��ֵ��С�����ֱ��DM��AC�Ľ���ʽ�����������鼴�ɽ�����⣮
����ʱP��F+EF+DE��ֵ��С�����ֱ��DM��AC�Ľ���ʽ�����������鼴�ɽ�����⣮
��3����ͼ3�У���NC=NMʱ���ɵ�����MNCQ����ֱ�����������ON��������εı߳����ɽ�����⣮
��1����ͼ1�У���HK��OA��K
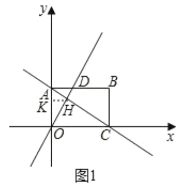
��OA=![]() ��OC=
��OC=![]() OA=3��
OA=3��
��A(0��![]() )��B(3��0)��
)��B(3��0)��
��ֱ��AC�Ľ���ʽΪy=kx+b������
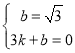
���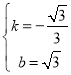
��ֱ��AC�Ľ���ʽΪ![]()
��tan��OAC=![]()
���OAC=![]()
��OD��AC��H��
���AHO=![]()
���AOH=![]()
��OH=OAcos![]() =
=![]()
��HK��OA��
��HK=![]() OH=
OH=![]() ��OK=
��OK=![]() HK=
HK=![]()
��H(![]() ��
��![]() )��
)��
�ʴ�Ϊ��![]() ��H(
��H(![]() ��
��![]() )
)
��2����ͼ2�У�
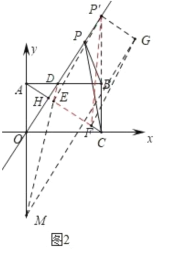
��|PCPB|BC��
�൱��P��CB���ӳ�����ʱ��|PCPB|��ֵ���ʱP��(3��![]() )��
)��
��P��G��AC��ʹ��P��G=EF=![]() ����ʱ
����ʱ![]()
��G����ֱ��AC�ĶԳƵ�M������DM��AC��E��GM��AC��![]() ����ʱP��F+EF+DE��ֵ��С��
����ʱP��F+EF+DE��ֵ��С��
��GJ=JM����M(m��n)��
����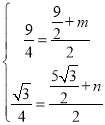
���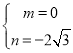
��M(0��![]() )����D(1��
)����D(1��![]() )��
)��
��ֱ��DM�Ľ���ʽΪ![]()
��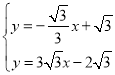
���
��![]()
�ʴ�Ϊ��![]()
��3����ͼ3�У�
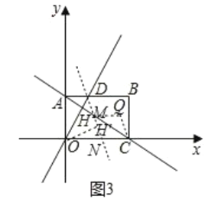
��NC=NMʱ���ɵ�����MNCQ
��NC=NM��
���NCM=��NMC=![]()
���ONM=��NCM+��NMC=![]()
��OH��=OH=![]() ��
��
��ON=OH��cos![]() =
=![]() ��
��
��CN=CQ=HN=HQ=3![]() ��
��
��Q(![]() ��
��![]() )
)
�ʴ𰸣����ڣ�Q(![]() ��
��![]() )
)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ�� ![]() ����2�����ݵ�x��
����2�����ݵ�x�� ![]() ʱ��y��x���������С����a+b+c��0��ȷ���У� ��
ʱ��y��x���������С����a+b+c��0��ȷ���У� ��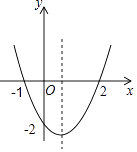
A.3��
B.4��
C.5��
D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB//EG//x�ᣬBC//DE//HG//AP//y�ᣬ��D��C��P��H��x���ϣ�A(1��2)��B(-1��2)��D(-3��0)��E(-3��-2)��G(3��-2)����һ����Ϊ2019����λ������û�е��Ե�ϸ�ߣ���ϸ���Բ��ƣ���һ�˹̶��ڵ�A��������A-B-C-D-E-F-G-H-P-A���Ĺ��ɽ�����ͼ�Ρ����ı��ϣ���ϸ����һ������λ�õĵ�������ǣ� ��

A.(1��2)B.(-1��2)C.(-1��-2)D.(1��1)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5��12�����ҹ���11��ȫ�����ּ����գ�����ij��ѧΪ�ռ��ƹ�ȫ����ּ���֪ʶ�ͱ����Ծȼ��ܣ���չ��������ֺ���������������������ȫ������֪ʶ���������һ�������꼶��500�ˣ�Ϊ�˵��龺�������ѧУ�����˳������飬�������£�����ݱ���ش����⣮
�ռ����ݣ�
�ӳ�һ�������꼶����ȡ20��ͬѧ�IJ��Գɼ�����λ���֣�����¼���£�
��һ��68��79��100��98��98��86��88��99��100��93��90��100��80��76��84��98��99��86��98��90
������92��89��100��99��98��94��100��62��100��86��75��98��89��100��100��68��79��100��92��89
�������ݣ�
��һ
������ |
|
|
|
|
��һ���� | 1 |
|
| 12 |
�������� | 2 | 2 | 4 | 12 |
�������ݣ�
����
���� | ƽ���� | ��λ�� | ���� | |
��һ | 90.5 | 91.5 |
| 84.75 |
���� | 90.5 |
| 100 | 123.05 |
�ó����ۣ�
��1���ڱ��У�![]() _______��
_______��![]() _______��
_______��![]() _______��
_______��![]() _______��
_______��
��2���÷�������ȶ�����___________�����һ���������
��3�����Ƹ�У��һ�������꼶ѧ�����β��Գɼ��п��Ե����ֵ��������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��l��m���ȱߡ�ABC�Ķ���B��ֱ��m�ϣ���BC��ֱ��m�������Ϊ20�㣬��Ϧ��Ķ���Ϊ�� ��
A.60��![]()
B.45��
C.40��
D.30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������ֽƬ��
��1����ͼ1����������ֽƬ�����Ϊ1dm2����������εĶԽ���AC�ij�Ϊ�� ��dm��
��2����һԲ���������������ε��������2��cm2����Բ���ܳ�ΪCԲ�������ε��ܳ�ΪC������CԲ�� ��C��(���������������)
��3����ͼ2���������ε����Ϊ16cm2������ͬѧ������������αߵķ���ó�һ�����Ϊ12cm2�ij�����ֽƬ��ʹ���ij��Ϳ�֮��Ϊ3��2�����ܲó�����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��б��BCΪ�ߣ�����ABC��ͬ����������BCEF���������ε�����ΪO������AO����AB��4��AO��6![]() ����AC�ij����ڣ�������
����AC�ij����ڣ�������

A. 12![]() B. 16C. 8+6
B. 16C. 8+6![]() D. 4+6
D. 4+6![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������Ҫ����ij�أ������������������乫˾�ļס������ֻ�������֪��ȥ�����������ֻ�����������±���

�����øù�˾3�����ֻ�����5�����ֻ���һ�θպ������������������ÿ�ָ��˷�30Ԫ���㣬����Ӧ���˷Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ�ף�![]() ��
��![]() ��
��![]() �Ĺ�ϵ��ʲô����д���������̣�
�Ĺ�ϵ��ʲô����д���������̣�
��2����ͼ�ң�![]() ��ֱ��д��
��ֱ��д��![]() ��
��![]() ��������ϵ_______________________��
��������ϵ_______________________��
��3����ͼ����![]() ��ֱ��д��
��ֱ��д��![]() ��
��![]() ��������ϵ_____________________��
��������ϵ_____________________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com