
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,点
如图,点![]() 是直线
是直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 面积最大时,请求出点
面积最大时,请求出点![]() 的坐标和
的坐标和![]() 面积的最大值?
面积的最大值?
![]() 在
在![]() 的结论下,过点
的结论下,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是抛物线对称轴上的动点,在抛物线上是否存在点
是抛物线对称轴上的动点,在抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?如果存在,请直接写出点
为顶点的四边形是平行四边形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.

【答案】(1)![]() ;(2)当
;(2)当![]() 时,即点
时,即点![]() 的坐标是
的坐标是![]() 时,
时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 、
、![]() 、
、![]() .
.
【解析】
(1)首先根据直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,求出点B的坐标是(0,3),点C的坐标是(4,0);然后根据抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,求出点B的坐标是(0,3),点C的坐标是(4,0);然后根据抛物线y=ax2+![]() x+c经过B、C两点,求出a\c的值是多少,即可求出抛物线的解析式.
x+c经过B、C两点,求出a\c的值是多少,即可求出抛物线的解析式.
(2)首先过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,然后设点E的坐标是(x,﹣![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣
x+3),则点M的坐标是(x,﹣![]() x+3),求出EM的值是多少;最后根据三角形的面积的求法,求出S△ABC,进而判断出当△BEC面积最大时,点E的坐标和△BEC面积的最大值各是多少即可.
x+3),求出EM的值是多少;最后根据三角形的面积的求法,求出S△ABC,进而判断出当△BEC面积最大时,点E的坐标和△BEC面积的最大值各是多少即可.
(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以P、Q、A、M为顶点的四边形是平行四边形的点P的坐标是多少即可.
(1)∵直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0).
x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0).
∵抛物线y=ax2+![]() x+c经过B、C两点,∴
x+c经过B、C两点,∴ ,解得:
,解得: ,∴y=﹣
,∴y=﹣![]() x2+
x2+![]() x+3.
x+3.
(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F.

∵点E是直线BC上方抛物线上的一动点,∴设点E的坐标是(x,﹣![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣
x+3),则点M的坐标是(x,﹣![]() x+3),∴EM=﹣
x+3),∴EM=﹣![]() x2+
x2+![]() x+3﹣(﹣
x+3﹣(﹣![]() x+3)=﹣
x+3)=﹣![]() x2+
x2+![]() x,∴S△BEC=S△BEM+S△MEC
x,∴S△BEC=S△BEM+S△MEC
=![]() =
=![]() ×(﹣
×(﹣![]() x2+
x2+![]() x)×4=﹣
x)×4=﹣![]() x2+3x=﹣
x2+3x=﹣![]() (x﹣2)2+3
(x﹣2)2+3
∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.
(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.
①如图2,由(2),可得点M的横坐标是2.

∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ).
).
又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是:![]() ;
;
∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则
解得: 或
或 .
.
∵x<0,∴点P的坐标是(﹣3,﹣![]() ).
).
②如图3,由(2),可得点M的横坐标是2.

∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ).
).
又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是:![]() ;
;
∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则
解得: 或
或 .
.
∵x>0,∴点P的坐标是(5,﹣![]() ).
).
③如图4,由(2),可得点M的横坐标是2.

∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ).
).
又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() .
.
∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则 ,解得:
,解得: ,∴点P的坐标是(﹣1,
,∴点P的坐标是(﹣1,![]() ).
).
综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣![]() )、(5,﹣
)、(5,﹣![]() )、(﹣1,
)、(﹣1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,山顶建有一座铁塔,塔高BC=80米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为45°,塔顶C点的仰角为60°.已测得小山坡的坡角为30°,坡长MP=40米.求山的高度AB(精确到1米).(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.

求证:△CED是等腰直角三角形
证明:∵∠1=∠2( )
∴EC= (在一个三角形中,等角对等边)
∵∠A=∠B=90°,AE=BC
∴△AED≌△BCE( )
∴∠AED=∠ ( )
∵∠BCE+∠BEC=90°
∠ +∠BEC=90°(等量代换)
∴∠DEC=90°.
∴△CED是等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:x2﹣6x=(x2﹣6x+9)﹣9=(x﹣3)2﹣9;﹣x2+10=﹣(x2﹣10x+25)+25=﹣(x﹣5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
(1)按上面材料提示的方法填空:a2﹣4a= = .﹣a2+12a= = .
(2)探究:当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值?请说明理由.
(3)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当三角形中一个内角![]() 是另一个内角
是另一个内角![]() 的2倍时,则称此三角形为“倍角三角形”,其中角
的2倍时,则称此三角形为“倍角三角形”,其中角![]() 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
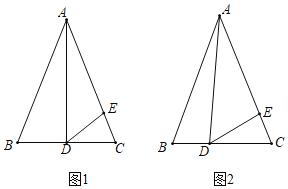
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B. C.E在同一条直线上,连结DC.

(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com