
ЁОЬтФПЁПФГЮФОпЕъФГМИжжаЭКХЕФМЦЫуЦїУПжЛНјМл 12 дЊЁЂЪлМл 20 дЊЃЌЖрТђгХЛнЃЌ гХЛнЗНЗЈЪЧЃКЗВЪЧвЛДЮТђ 10 жЛвдЩЯЕФЃЌУПЖрТђвЛжЛЃЌЫљТђЕФШЋВПМЦЫуЦїУПжЛОЭ НЕМл 0.1 дЊЃЌР§ШчЃКФГШЫТђ 18 жЛМЦЫуЦїЃЌгкЪЧУПжЛНЕМл 0.1ЁС(18Ѓ10)ЃН0.8(дЊ)ЃЌ вђДЫЫљТђЕФ 18 жЛМЦЫуЦїЖМАДУПжЛ 19.2 дЊЕФМлИёЙКТђЃЌЕЋЪЧУПжЛМЦЫуЦїЕФзюЕЭЪл МлЮЊ 16 дЊЃЎ
(1)ЧѓвЛДЮжСЩйЙКТђЖрЩйжЛМЦЫуЦїЃЌВХФмвдзюЕЭЪлМлЙКТђЃП (2)аДГіИУЮФОпЕъвЛДЮЯњЪл x(xЃО10)жЛЪБЃЌЫљЛёРћШѓ y(дЊ)гы x(жЛ)жЎМфЕФКЏЪ§ЙиЯЕ ЪНЃЌВЂаДГіздБфСП x ЕФШЁжЕЗЖЮЇЃЛ
(3)вЛЬьЃЌМзЙЫПЭЙКТђСЫ 46 жЛЃЌввЙЫПЭЙКТђСЫ 50 жЛЃЌЕъжїЗЂЯжТє 46 жЛзЌЕФЧЎЗД ЖјБШТє 50 жЛзЌЕФЧЎЖрЃЌЧыФуЫЕУїЗЂЩњетвЛЯжЯѓЕФдвђЃЛЕБ 10ЃМxЁм50 ЪБЃЌЮЊСЫ ЛёЕУзюДѓРћШѓЃЌЕъМввЛДЮгІТєЖрЩйжЛЃПетЪБЕФЪлМлЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉвЛДЮжСЩйТђ50жЛЃЌВХФмвдзюЕЭМлЙКТђЃЛЃЈ2ЃЉy=![]() ЃЛЃЈ3ЃЉдвђЯъМћНтЮіЃЌзюЕЭЪлМлЮЊ16.5дЊЃЌРћШѓзюДѓЃЌДЫЪБгІТє45жЛЃЎ
ЃЛЃЈ3ЃЉдвђЯъМћНтЮіЃЌзюЕЭЪлМлЮЊ16.5дЊЃЌРћШѓзюДѓЃЌДЫЪБгІТє45жЛЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшвЛДЮЙКТђxжЛЃЌгЩгкЗВЪЧвЛДЮТђ10жЛвдЩЯЕФЃЌУПЖрТђвЛжЛЃЌЫљТђЕФШЋВПМЦЫуЦїУПжЛОЭНЕЕЭ0.1дЊЃЌЖјзюЕЭМлЮЊУПжЛ16дЊЃЌвђДЫЕУЕН20-0.1ЃЈx-10ЃЉ=16ЃЌНтЗНГЬМДПЩЧѓНтЃЛЃЈ2ЃЉЗж10ЃМxЁм5КЭxЃО50СНжжЧщПіЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛЃЈ3ЃЉАбКЏЪ§НтЮіЪНy=-0.1x2+9xЛЏЮЊЖЅЕуЪНy=-0.1ЃЈx-45ЃЉ2+202.5ЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФдіМѕадЃЌдйНсКЯвбжЊЬѕМўМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉЩшвЛДЮЙКТђxжЛЃЌ
дђ20-0.1ЃЈx-10ЃЉ=16ЃЌ
НтЕУЃКx=50ЃЎ
Д№ЃКвЛДЮжСЩйТђ50жЛЃЌВХФмвдзюЕЭМлЙКТђЃЛ
ЃЈ2ЃЉЕБ10ЃМxЁм50ЪБЃЌy=[20-0.1ЃЈx-10ЃЉ-12]x=-0.1x2+9xЃЌ
ЕБxЃО50ЪБЃЌy=ЃЈ16-12ЃЉx=4xЃЛ
злЩЯЫљЪіЃКy=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉy=-0.1x2+9x=-0.1ЃЈx-45ЃЉ2+202.5ЃЌ
ЂйЕБ10ЃМxЁм45ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌМДЕБТєЕФжЛЪ§дНЖрЪБЃЌРћШѓИќДѓЃЎ
ЂкЕБ45ЃМxЁм50ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌМДЕБТєЕФжЛЪ§дНЖрЪБЃЌРћШѓБфаЁЃЎ
ЧвЕБx=46ЪБЃЌy1=202.4ЃЌ
ЕБx=50ЪБЃЌy2=200ЃЎ
y1ЃОy2ЃЎ
МДГіЯжСЫТє46жЛзЌЕФЧЎБШТє50жЛзЌЕФЧЎЖрЕФЯжЯѓЃЎ
ЕБx=45ЪБЃЌзюЕЭЪлМлЮЊ20-0.1ЃЈ45-10ЃЉ=16.5ЃЈдЊЃЉЃЌРћШѓзюДѓЃЌДЫЪБгІТє45жЛЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбДѓаЁКЭаЮзДЭъШЋЯрЭЌЕФ![]() еХПЈЦЌЗжГЩСНзщЃЌУПзщ
еХПЈЦЌЗжГЩСНзщЃЌУПзщ![]() еХЃЌЗжБ№БъЩЯ
еХЃЌЗжБ№БъЩЯ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌНЋетСНзщПЈЦЌЗжБ№ЗХШыСНИіКазгжаНСдШЃЌдйДгжаЫцЛњГщШЁвЛеХЃЎ
ЃЌНЋетСНзщПЈЦЌЗжБ№ЗХШыСНИіКазгжаНСдШЃЌдйДгжаЫцЛњГщШЁвЛеХЃЎ
![]() ЧыгУЛЪїзДЭМЕФЗНЗЈЧѓШЁГіЕФСНеХПЈЦЌЪ§зжжЎКЭЮЊЦцЪ§ЕФИХТЪЃЛ
ЧыгУЛЪїзДЭМЕФЗНЗЈЧѓШЁГіЕФСНеХПЈЦЌЪ§зжжЎКЭЮЊЦцЪ§ЕФИХТЪЃЛ
![]() ШєШЁГіЕФСНеХПЈЦЌЪ§зжжЎКЭЮЊЦцЪ§ЃЌдђМзЪЄЃЛШЁГіЕФСНеХПЈЦЌЪ§зжжЎКЭЮЊХМЪ§ЃЌдђввЪЄЃЛЪдЗжЮіетИігЮЯЗЪЧЗёЙЋЦНЃПЧыЫЕУїРэгЩЃЎ
ШєШЁГіЕФСНеХПЈЦЌЪ§зжжЎКЭЮЊЦцЪ§ЃЌдђМзЪЄЃЛШЁГіЕФСНеХПЈЦЌЪ§зжжЎКЭЮЊХМЪ§ЃЌдђввЪЄЃЛЪдЗжЮіетИігЮЯЗЪЧЗёЙЋЦНЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈЉ1ЃЌ5ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌCЃЈЉ4ЃЌ3ЃЉЃЎ

ЃЈ1ЃЉдкЭМжаЕФЕуЩЯБъГіЯргІзжФИAЁЂBЁЂCЃЌВЂЧѓГіЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉдкЭМжазїГіЁїABCЙигкyжсЕФЖдГЦЭМаЮЁїA1B1C1ЃЛ
ЃЈ3ЃЉаДГіЕуA1ЃЌB1ЃЌC1ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЫФБпаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЃЌ
ЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЁЂ
ЁЂ![]() ЪЧ
ЪЧ![]() ЩЯСНЖЏЕуЃЌ
ЩЯСНЖЏЕуЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№Дг
ЗжБ№Дг![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБвд
СНЕуЭЌЪБвд![]() ЕФЯрЭЌЕФЫйЖШЯђ
ЕФЯрЭЌЕФЫйЖШЯђ![]() ЁЂ
ЁЂ![]() дЫЖЏ
дЫЖЏ

![]() ЫФБпаЮ
ЫФБпаЮ![]() ЪЧЦНааЫФБпаЮТ№ЃПЫЕУїФуЕФРэгЩЃЎ
ЪЧЦНааЫФБпаЮТ№ЃПЫЕУїФуЕФРэгЩЃЎ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌЕБдЫЖЏЪБМф
ЃЌЕБдЫЖЏЪБМф![]() ЮЊЖрЩйЪБЃЌвд
ЮЊЖрЩйЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊОиаЮЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЮЊОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2+ЃЈkЉ5ЃЉx+1Љk=0ЃЈЦфжаkЮЊГЃЪ§ЃЉ.
ЃЈ1ЃЉЧѓжЄЮоТлkЮЊКЮжЕЃЌЗНГЬзмгаСНИіВЛЯрЕШЪЕЪ§ИљЃЛ
ЃЈ2ЃЉвбжЊКЏЪ§y=x2+ЃЈkЉ5ЃЉx+1ЉkЕФЭМЯѓВЛОЙ§ЕкШ§ЯѓЯоЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєдЗНГЬЕФвЛИіИљДѓгк3ЃЌСэвЛИіИљаЁгк3ЃЌЧѓkЕФзюДѓећЪ§жЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌЁЯA=ЁЯB=30ЁуЃЌE,F дк AB ЩЯЃЌЁЯECF=60Ёу.
ЃЈ1ЃЉЛГіЁїBCF ШЦЕу C ЫГЪБеыа§зЊ 120ЁуКѓЕФЁїACKЃЛ
ЃЈ2ЃЉдк(1)жаЃЌШє AE2ЃЋ EF2ЃН BF2ЃЌЧѓжЄ BFЃН![]() CF.
CF.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌЕуPЪЧЩфЯпONЩЯвЛЖЏЕуЃЌЕуBЪЧЩфЯпOAЩЯвЛЖЏЕуЃЌЕуBЃЌPОљВЛгыЕуOжиКЯЃЌЕБ
ЃЌЕуPЪЧЩфЯпONЩЯвЛЖЏЕуЃЌЕуBЪЧЩфЯпOAЩЯвЛЖЏЕуЃЌЕуBЃЌPОљВЛгыЕуOжиКЯЃЌЕБ![]() _____ЪБЃЌ
_____ЪБЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЛШчЙћЪЙЕУ
ЮЊжБНЧШ§НЧаЮЃЛШчЙћЪЙЕУ![]() ЮЊЖлНЧШ§НЧаЮЃЌдђ
ЮЊЖлНЧШ§НЧаЮЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ_____.
ЕФШЁжЕЗЖЮЇЪЧ_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаУќЬтжаЃЌаДГіЦфФцУќЬтЃЌВЂХаЖЯФцУќЬтЕФецМй.
ЃЈ1ЃЉШчЙћСНИіНЧЯрЕШЃЌФЧУДЫќУЧЖМЪЧЖдЖЅНЧЃЛ
ЃЈ2ЃЉжБНЧЖМЯрЕШЃЛ
ЃЈ3ЃЉСНЬѕЦНааЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌЫљГЩЕФЭЌЮЛНЧЯрЕШЃЛ
ЃЈ4ЃЉШчЙћ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЃЛ
ЃЛ
ЃЈ5ЃЉШчЙћвЛИіШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌФЧУДЫќЕФСНИіШёНЧЛЅгр.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌDEЁЂDFЗжБ№ЪЧЁїABDКЭЁїACDЕФИпЁЃЧѓжЄЃКADДЙжБЦНЗжEFЁЃ
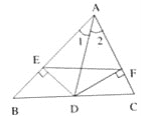
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com