
【题目】平行四边形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() 、
、![]() 是
是![]() 上两动点,
上两动点,![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以
两点同时以![]() 的相同的速度向
的相同的速度向![]() 、
、![]() 运动
运动

![]() 四边形
四边形![]() 是平行四边形吗?说明你的理由.
是平行四边形吗?说明你的理由.
![]() 若
若![]() ,
,![]() ,当运动时间
,当运动时间![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形.
为顶点的四边形为矩形.
【答案】(1)见解析;(2) t为2s时.
【解析】
(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:18-2t-2t=10,继而求得答案.
解:![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
理由:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵![]() 、
、![]() 是
是![]() 上两动点,
上两动点,![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以
两点同时以![]() 的相同的速度向
的相同的速度向![]() 、
、![]() 运动,
运动,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
![]() 根据题意得:
根据题意得:![]() 或
或![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴当![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
即![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
解得:![]() ,
,
∴当运动时间![]() 为
为![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM=AN,点B和点C分别为∠MAN两边上的点,AB=AC.按下列语句画出图形:(要求用无刻度直尺作图,)
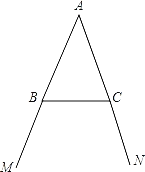
(1)AD⊥BC,垂足为D;
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的三边为边分别作等边
的三边为边分别作等边![]() 、
、![]() 、
、![]() ,则下列结论:①①
,则下列结论:①①![]() ;②四边形
;②四边形![]() 为平行四边形;③当
为平行四边形;③当![]() 时,四边形
时,四边形![]() 是菱形;④当
是菱形;④当![]() 时,四边形
时,四边形![]() 是矩形.其中正确的结论有( )个.
是矩形.其中正确的结论有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店某几种型号的计算器每只进价 12 元、售价 20 元,多买优惠, 优惠方法是:凡是一次买 10 只以上的,每多买一只,所买的全部计算器每只就 降价 0.1 元,例如:某人买 18 只计算器,于是每只降价 0.1×(18-10)=0.8(元), 因此所买的 18 只计算器都按每只 19.2 元的价格购买,但是每只计算器的最低售 价为 16 元.
(1)求一次至少购买多少只计算器,才能以最低售价购买? (2)写出该文具店一次销售 x(x>10)只时,所获利润 y(元)与 x(只)之间的函数关系 式,并写出自变量 x 的取值范围;
(3)一天,甲顾客购买了 46 只,乙顾客购买了 50 只,店主发现卖 46 只赚的钱反 而比卖 50 只赚的钱多,请你说明发生这一现象的原因;当 10<x≤50 时,为了 获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等边三角形,点E在线段AB上,点D在直线BC上,且
是等边三角形,点E在线段AB上,点D在直线BC上,且![]() ,将
,将![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() 至
至![]() ,连接EF.
,连接EF.
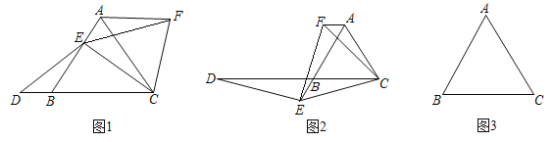
(1)证明:![]() ;
;
(2)如图2,如果点E在线段AB的延长线上,其他条件不变,请你写出线段AB、DB、AF之间的数量关系,并证明你的结论;
(3)如果点E在线段BA的延长线上,其他条件不变,请在图3的基础上将图形补充完整,并写出AB、DB、AF之间的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售服装,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价
元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价![]() 元,每天可多售出
元,每天可多售出![]() 件.
件.
![]() 设每件降价
设每件降价![]() 元,每天盈利
元,每天盈利![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;![]() 若商场每天要盈利
若商场每天要盈利![]() 元,同时尽量减少库存,每件应降价多少元?
元,同时尽量减少库存,每件应降价多少元?
![]() 每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com