
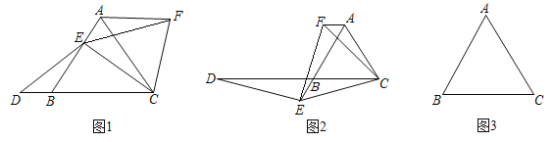
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊ![]() ЪЧЕШБпШ§НЧаЮЃЌЕуEдкЯпЖЮABЩЯЃЌЕуDдкжБЯпBCЩЯЃЌЧв
ЪЧЕШБпШ§НЧаЮЃЌЕуEдкЯпЖЮABЩЯЃЌЕуDдкжБЯпBCЩЯЃЌЧв![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕуCЫГЪБеыа§зЊ
ШЦЕуCЫГЪБеыа§зЊ![]() жС
жС![]() ЃЌСЌНгEF.
ЃЌСЌНгEF.
ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШчЙћЕуEдкЯпЖЮABЕФбгГЄЯпЩЯЃЌЦфЫћЬѕМўВЛБфЃЌЧыФуаДГіЯпЖЮABЁЂDBЁЂAFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉШчЙћЕуEдкЯпЖЮBAЕФбгГЄЯпЩЯЃЌЦфЫћЬѕМўВЛБфЃЌЧыдкЭМ3ЕФЛљДЁЩЯНЋЭМаЮВЙГфЭъећЃЌВЂаДГіABЁЂDBЁЂAFжЎМфЕФЪ§СПЙиЯЕЃЌВЛБижЄУї.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉABЃНBDЉAFЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉВЙГфЭМаЮМћНтЮіЃЌABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуEзїEGЁЮBCНЛACгкЕуGЃЌПЩЕУЁїAEGЮЊЕШБпШ§НЧаЮЃЌНјЖјПЩЕУBE=CGЃЌвзжЄЁЯBEDЃНЁЯGCEЃЌдйИљОнSASПЩжЄЁїBDEЁеЁїGECЃЌПЩЕУBDЃНEGЃНAEЃЌНјвЛВНМДЕУНсТлЃЛ
ЃЈ2ЃЉНсТлЃКABЃНBDЉAFЃЛШчЭМ2ЃЌбгГЄEFЁЂCAНЛгкЕуGЃЌЯШгЩа§зЊЕФаджЪжЄЕУЁїCEFЪЧЕШБпШ§НЧаЮЃЌНјЖјПЩЭЦЕУEDЃНEFЃЌШЛКѓРћгУШ§НЧаЮЕФЭтНЧаджЪПЩЭЦЕУЁЯFCGЃНЁЯFEAЃЌНјЖјПЩЕУЁЯDЃНЁЯFEAЃЌвзжЄЁЯDBEЃНЁЯFAEЃН60ЁуЃЌгкЪЧИљОнAASПЩжЄЁїEDBЁеЁїFEAЃЌПЩЕУBDЃНAEЃЌНјвЛВНИљОнЕШЯпЖЮДњЛЛМДПЩжЄЕУНсТлЃЛ
ЃЈ3ЃЉABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎШчЭМ3жаЃЌЯШИљОна§зЊЕФаджЪХаЖЯЁїCEFЪЧЕШБпШ§НЧаЮЃЌПЩЕУEFЃНECЃЌНјЖјПЩЕУEDЃНEFЃЌШЛКѓИљОнШ§НЧаЮЕФЭтНЧаджЪКЭНЧЖШжЎМфЕФЙиЯЕПЩЕУЁЯBDEЃНЁЯAEFЃЌвзжЄЁЯBЃНЁЯEAFЃН60ЁуЃЌгкЪЧИљОнAASПЩжЄЁїEDBЁеЁїFEAЃЌПЩЕУBDЃНAEЃЌEBЃНAFЃЌНјвЛВНМДПЩжЄЕУНсТл.
НтЃКЃЈ1ЃЉжЄУїЃКЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрAB=AC=BCЃЌЁЯABCЃНЁЯBCAЃН60ЁуЃЌ
ЁпЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌЁрBEЃНAFЃЌ
ШчЭМ1ЃЌЙ§ЕуEзїEGЁЮBCНЛACгкЕуGЃЌдђЁїAEGЮЊЕШБпШ§НЧаЮЃЌЁрAE=AG=EGЃЌЁрBE=CGЃЌ
ЁпDEЃНCEЃЌЁрЁЯCDEЃНЁЯECDЃЌ
гжЁпЁЯCDE+ЁЯBEDЃНЁЯABCЃНЁЯACDЃНЁЯECD+ЁЯGCEЃЌ
ЁрЁЯBEDЃНЁЯGCEЃЌ
дкЁїBDEКЭЁїGECжаЃЌ
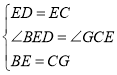 ЃЌ
ЃЌ
ЁрЁїBDEЁеЁїGECЃЈSASЃЉЃЌ
ЁрBDЃНEGЃНAEЃЌ
гжЁпAFЃНBEЃЌ
ЁрABЃНBE+AEЃНAF+BDЃЛ
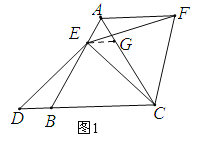
ЃЈ2ЃЉНсТлЃКABЃНBDЉAFЃЛ
РэгЩЃКШчЭМ2ЃЌбгГЄEFЁЂCAНЛгкЕуGЃЌ
ЁпЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌ
ЁрЁЯECFЃН60ЁуЃЌBEЃНAFЃЌECЃНCFЃЌ
ЁрЁїCEFЪЧЕШБпШ§НЧаЮЃЌЁрEFЃНECЃЌ
гжЁпEDЃНECЃЌЁрEDЃНEFЃЌЁЯEFCЃНЁЯBACЃН60ЁуЃЌ
ЁпЁЯEFCЃНЁЯG+ЁЯFCGЃЌЁЯBACЃНЁЯG+ЁЯFEAЃЌ
ЁрЁЯFCGЃНЁЯFEAЃЌ
ЁпЁЯFCGЃНЁЯECDЃЌЁЯDЃНЁЯECDЃЌ
ЁрЁЯDЃНЁЯFEAЃЌ
гЩа§зЊЕФаджЪЕУЃКЁЯCBEЃНЁЯCAFЃН120ЁуЃЌгжЁпЁЯBAC=60ЁуЃЌ
ЁрЁЯDBEЃНЁЯFAEЃН60ЁуЃЌ
дкЁїEDBКЭЁїFEAжаЃЌ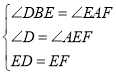 ЃЌ
ЃЌ
ЁрЁїEDBЁеЁїFEAЃЈAASЃЉЃЌ
ЁрBDЃНAEЃЌEBЃНAFЃЌ
ЁпAE=AB+BEЃЌ
ЁрBDЃНFA+ABЃЌ
МДABЃНBDЉAFЃЛ
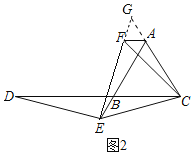
ЃЈ3ЃЉШчЭМ3жаЃЌABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎ
ЁпЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌ
ЁрЁЯECFЃН60ЁуЃЌBEЃНAFЃЌECЃНCFЃЌЁрЁїCEFЪЧЕШБпШ§НЧаЮЃЌЁрEFЃНECЃЌ
гжЁпEDЃНECЃЌЁрEDЃНEFЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBЃНЁЯBACЃН60ЁуЃЌ
гжЁпЁЯBЃНЁЯCAFЃЌЁрЁЯCAFЃН60ЁуЃЌ
ЁрЁЯEAFЃН180ЁуЉЁЯCAFЉЁЯBACЃН180ЁуЉ60ЁуЉ60ЁуЃН60ЁуЃЌ
ЁрЁЯBЃНЁЯEAFЃЛ
ЁпEDЃНECЃЌЁрЁЯECDЃНЁЯEDCЃЌ
ЁрЁЯBDEЃНЁЯECD+ЁЯDECЃНЁЯEDC+ЁЯDECЃЌ
гжЁпЁЯEDCЃНЁЯB+ЁЯBEDЃЌ
ЁрЁЯBDEЃНЁЯB+ЁЯBED+ЁЯDECЃН60Ёу+ЁЯBECЃЌ
ЁпЁЯAEFЃНЁЯCEF+ЁЯBECЃН60Ёу+ЁЯBECЃЌ
ЁрЁЯBDEЃНЁЯAEFЃЌ
дкЁїEDBКЭЁїFEAжаЃЌ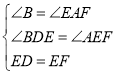 ЃЌ
ЃЌ
ЁрЁїEDBЁеЁїFEAЃЈAASЃЉЃЌ
ЁрBDЃНAEЃЌEBЃНAFЃЌ
ЁпBEЃНAB+AEЃЌ
ЁрAFЃНAB+BDЃЌ
МДABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЪЧЃКAFЃНAB+BDЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗДБШР§КЏЪ§y=![]() ЃЈaЃО0ЃЌaЮЊГЃЪ§ЃЉКЭy=
ЃЈaЃО0ЃЌaЮЊГЃЪ§ЃЉКЭy=![]() дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуMдкy=
дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуMдкy=![]() ЕФЭМЯѓЩЯЃЌMCЁЭxжсгкЕуCЃЌНЛy=
ЕФЭМЯѓЩЯЃЌMCЁЭxжсгкЕуCЃЌНЛy=![]() ЭМЯѓгкЕуAЃЛMDЁЭyжсгкЕуDЃЌНЛy=
ЭМЯѓгкЕуAЃЛMDЁЭyжсгкЕуDЃЌНЛy=![]() ЕФЭМЯѓгкЕуBЃЌЕБЕуMдкy=
ЕФЭМЯѓгкЕуBЃЌЕБЕуMдкy=![]() ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃКЂйSЁїODB=SЁїOCAЃЛЂкЫФБпаЮOAMBЕФУцЛ§ВЛБфЃЛЂлЕБЕуAЪЧMCЕФжаЕуЪБЃЌдђЕуBЪЧMDЕФжаЕуЃЎЦфжае§ШЗНсТлЕФађКХЪЧ___________;
ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃКЂйSЁїODB=SЁїOCAЃЛЂкЫФБпаЮOAMBЕФУцЛ§ВЛБфЃЛЂлЕБЕуAЪЧMCЕФжаЕуЪБЃЌдђЕуBЪЧMDЕФжаЕуЃЎЦфжае§ШЗНсТлЕФађКХЪЧ___________;

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЫФБпаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЃЌ
ЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЁЂ
ЁЂ![]() ЪЧ
ЪЧ![]() ЩЯСНЖЏЕуЃЌ
ЩЯСНЖЏЕуЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№Дг
ЗжБ№Дг![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБвд
СНЕуЭЌЪБвд![]() ЕФЯрЭЌЕФЫйЖШЯђ
ЕФЯрЭЌЕФЫйЖШЯђ![]() ЁЂ
ЁЂ![]() дЫЖЏ
дЫЖЏ

![]() ЫФБпаЮ
ЫФБпаЮ![]() ЪЧЦНааЫФБпаЮТ№ЃПЫЕУїФуЕФРэгЩЃЎ
ЪЧЦНааЫФБпаЮТ№ЃПЫЕУїФуЕФРэгЩЃЎ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌЕБдЫЖЏЪБМф
ЃЌЕБдЫЖЏЪБМф![]() ЮЊЖрЩйЪБЃЌвд
ЮЊЖрЩйЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊОиаЮЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЮЊОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌЁЯA=ЁЯB=30ЁуЃЌE,F дк AB ЩЯЃЌЁЯECF=60Ёу.
ЃЈ1ЃЉЛГіЁїBCF ШЦЕу C ЫГЪБеыа§зЊ 120ЁуКѓЕФЁїACKЃЛ
ЃЈ2ЃЉдк(1)жаЃЌШє AE2ЃЋ EF2ЃН BF2ЃЌЧѓжЄ BFЃН![]() CF.
CF.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌЕуPЪЧЩфЯпONЩЯвЛЖЏЕуЃЌЕуBЪЧЩфЯпOAЩЯвЛЖЏЕуЃЌЕуBЃЌPОљВЛгыЕуOжиКЯЃЌЕБ
ЃЌЕуPЪЧЩфЯпONЩЯвЛЖЏЕуЃЌЕуBЪЧЩфЯпOAЩЯвЛЖЏЕуЃЌЕуBЃЌPОљВЛгыЕуOжиКЯЃЌЕБ![]() _____ЪБЃЌ
_____ЪБЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЛШчЙћЪЙЕУ
ЮЊжБНЧШ§НЧаЮЃЛШчЙћЪЙЕУ![]() ЮЊЖлНЧШ§НЧаЮЃЌдђ
ЮЊЖлНЧШ§НЧаЮЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ_____.
ЕФШЁжЕЗЖЮЇЪЧ_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШбќRtЁїABCЃЌЁЯACB=90ЁуЃЌCA=CBЃЌвдBCЮЊБпЯђЭтзїЕШБпЁїCBAЃЌСЌНгADЃЌЙ§ЕуCзїЁЯACBЕФНЧЦНЗжЯпгыADНЛгкЕуEЃЌСЌНгBEЃЎ

ЃЈ1ЃЉШєAE=2ЃЌЧѓCEЕФГЄЖШЃЛ
ЃЈ2ЃЉвдABЮЊБпЯђЯТзїЁїAFBЃЌЁЯAFB=60ЁуЃЌСЌНгFEЃЌЧѓжЄЃКFA+FB= ![]() FEЃЎ
FEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаУќЬтжаЃЌаДГіЦфФцУќЬтЃЌВЂХаЖЯФцУќЬтЕФецМй.
ЃЈ1ЃЉШчЙћСНИіНЧЯрЕШЃЌФЧУДЫќУЧЖМЪЧЖдЖЅНЧЃЛ
ЃЈ2ЃЉжБНЧЖМЯрЕШЃЛ
ЃЈ3ЃЉСНЬѕЦНааЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌЫљГЩЕФЭЌЮЛНЧЯрЕШЃЛ
ЃЈ4ЃЉШчЙћ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЃЛ
ЃЛ
ЃЈ5ЃЉШчЙћвЛИіШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌФЧУДЫќЕФСНИіШёНЧЛЅгр.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌCA=CBЃЌCD=CEЃЌЁЯACB=ЁЯDCE=ІСЃЎ
ЃЈ1ЃЉЧѓжЄЃКBE=ADЃЛ

ЃЈ2ЃЉЕБІС=90ЁуЪБЃЌШЁADЃЌBEЕФжаЕуЗжБ№ЮЊЕуPЁЂQЃЌСЌНгCPЃЌCQЃЌPQЃЌШчЭМЂкЃЌХаЖЯЁїCPQЕФаЮзДЃЌВЂМгвджЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіВЛЭИУїЕФПкДќРязАгаЗжБ№БъгаККзжЁАЪщЁБЁЂЁА ЯуЁБЁЂЁА РњЁБЁЂЁА ГЧЁБЕФЫФИіаЁЧђЃЌГ§ККзжВЛЭЌжЎЭтЃЌаЁЧђУЛгаШЮКЮЧјБ№ЃЌУПДЮУўЧђЧАЯШНСАшОљдШЃЎ
ЃЈ1ЃЉШєДгжаШЮШЁвЛИіЧђЃЌЧђЩЯЕФККзжИеКУЪЧ ЁАЪщЁБЕФИХТЪЮЊ__________.
ЃЈ2ЃЉДгжаШЮШЁвЛЧђЃЌВЛЗХЛиЃЌдйДгжаШЮШЁвЛЧђЃЌЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓШЁГіЕФСНИіЧђЩЯЕФККзжФмзщГЩЁАРњГЧЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com