
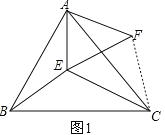
【题目】(1)如图 1 所示,△ ABC 和△ AEF 为等边三角形,点 E 在△ ABC 内部,且 E 到点 A、B、C 的距离分别为 3、4、5,求∠AEB 的度数.
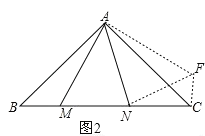
(2)如图 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 为 BC 上的两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°,得到△ACF.求证:MN![]() = NC
= NC![]() +BM
+BM![]() (提示:旋转前后的图形全等)
(提示:旋转前后的图形全等)
【答案】(1)∠AEB=150°;(2)见解析.
【解析】
(1)根据等边三角形的性质得出AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,求出∠BAE=∠CAF,证出△BAE≌△CAF,得出CF=BE=4,∠AEB=∠AFC,求出CE2=EF2+CF2,得出∠CFE=90°,即可得出结果;
(2)根据将△ABM绕A点逆时针旋转90°,得到△ACF,可知AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,求出∠NAF=∠MAN,证出△MAN≌△FAN,得出MN=FN,求出∠FCN=90°,由勾股定理得出NF2=CF2+CN2即可解决问题.
解:(1)如图1所示:
∵△ABC和△AEF为等边三角形,
∴AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,
∴∠BAE=∠CAF=60°∠CAE,
在△BAE和△CAF中,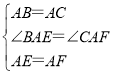 ,
,
∴△BAE≌△CAF(SAS),
∴CF=BE=4,∠AEB=∠AFC,
∴EF=3,CE=5,
∴CE2=EF2+CF2,
∴∠CFE=90°
∵∠AFE=60°,
∴∠AFC=90°+60°=150°,
∴∠AEB=∠AFC=150°;
(2)如图2所示:
∵将△ABM绕A点逆时针选择90°,得到△ACF,
∴AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,
∵∠BAC=90°,∠MAN=45°,
∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°45°=45°=∠MAN,
在△MAN和△FAN中,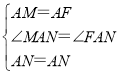 ,
,
∴△MAN≌△FAN(SAS),
∴MN=FN,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵∠B=∠ACF,
∴∠ACF=45°,
∴∠FCN=90°,
由勾股定理得:NF2=CF2+CN2,
∵CF=BM,NF=MN,
∴MN2=NC2+BM2.


科目:初中数学 来源: 题型:
【题目】如图,有一块铁皮,拱形边缘呈抛物线状,MN=4,抛物线顶点处到边MN的距离是4,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上.
(1)如图建立适当的坐标系,求抛物线解析式;
(2)设矩形ABCD的周长为L,点C的坐标为(m,0),求L与m的关系式(不要求写自变量取值范围).
(3)问这样截下去的矩形铁皮的周长能否等于9.5,若不等于9.5,请说明理由,若等于9.5,求出吗的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的父亲在相距![]() 米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是
米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是![]() 米,绳子自然下垂呈抛物线状,身高
米,绳子自然下垂呈抛物线状,身高![]() 米的小明距较近的那棵树
米的小明距较近的那棵树![]() 米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着私家车的增加,交通也越来越拥挤,通常情况下,某段公路上车辆的行驶速度(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当x≥8时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )

A. x<32 B. x≤32 C. x>32 D. x≥32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=![]() (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )

A. 1 B. ![]() C. 2
C. 2![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() 可以转化为指数式
可以转化为指数式![]() .
.
根据以上材料,解决下列问题:
(1)计算:![]() ,
,![]() ,
,![]() ;
;
(2)观察(1)中的三个数,猜测:![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ),并加以证明这个结论;
),并加以证明这个结论;
(3)已知:![]() ,求
,求![]() 和
和![]() 的值(
的值(![]() 且
且![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.
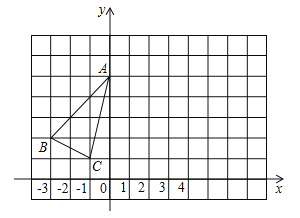
(1)画出△ABC关于y轴对称的△AB1C1, 并写出B1的坐标;
(2)将△ABC向右平移8个单位, 画出平移后的△A2B2C2, 写出B2的坐标;
(3)认真观察所作的图形, △AB1C1与△A2B2C2有怎样的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com