
【题目】已知△ABC在平面直角坐标系中的位置如图所示.
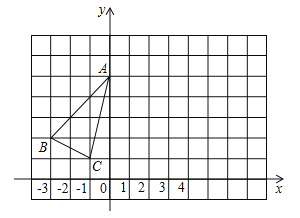
(1)画出△ABC关于y轴对称的△AB1C1, 并写出B1的坐标;
(2)将△ABC向右平移8个单位, 画出平移后的△A2B2C2, 写出B2的坐标;
(3)认真观察所作的图形, △AB1C1与△A2B2C2有怎样的位置关系.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图 1 所示,△ ABC 和△ AEF 为等边三角形,点 E 在△ ABC 内部,且 E 到点 A、B、C 的距离分别为 3、4、5,求∠AEB 的度数.
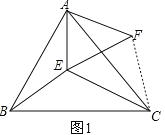
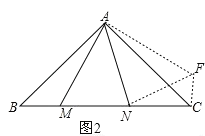
(2)如图 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 为 BC 上的两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°,得到△ACF.求证:MN![]() = NC
= NC![]() +BM
+BM![]() (提示:旋转前后的图形全等)
(提示:旋转前后的图形全等)
查看答案和解析>>
科目:初中数学 来源: 题型:
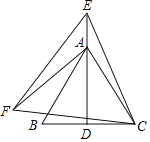
【题目】如图,D为等边△ABC中边BC的中点,在边DA的延长线上取一点E,以CE为边、在CE的左下方作等边△CEF,连结AF.若AB=4,AF=![]() ,则CF的值为_____.
,则CF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的图象(折线ABCDE)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为![]() 千米/时;
千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c的图像与x 轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图像上,CD//x轴,且CD=2,直线l 是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c 的值;
(2)如图①,连接BE,线段OC 上的点F 关于直线l 的对称点F′ 恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P 作x 轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
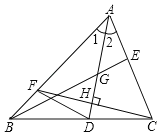
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法正确的是_____(填序号).
①D是BC的中点;②∠CDA>∠2;③BE是△ABC的边AC上的中线;
④CH为△ACD的边AD上的高;⑤△AFC为等腰三角形;
⑥连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如图1,求证∠BAC=∠B+2∠E;
(2)如图2,过点A作AF⊥BC,垂足为点F,若∠DCE=2∠CAF,∠B=2∠E,求∠BAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
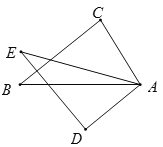
【题目】如图,已知,![]() ,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③
,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③![]() ;④
;④ ![]() .其中能使
.其中能使![]() 的条件为__________ (注:把你认为正确的答案序号都填上).
的条件为__________ (注:把你认为正确的答案序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com