
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
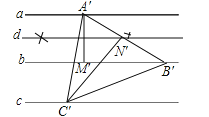
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.


【答案】(1)∠ABC=60°;
(2)证明见解析;
(3)△AEB可以看作是由△ADC绕点A顺时针旋转60°得到的,△AED是等边三角形;
(4)作图及画图过程见解析.
【解析】试题分析:
(1)连接BC,通过证明△ABC是等边三角形,即可求出∠ABC的度数;
(2)在Rt△AEB与Rt△ADC中,通过HL证明△AEB≌△ADC;
(3)由旋转的性质即可得出△AED是等边三角形;
(4)利用HL定理可证△A′N′C′≌△A′M′B′,得∠C′A′N′=∠B′A′M′,于是∠B′A′C′=∠M′A′N′=60°,由A′B′=A′C′得△A′B′C′为等边三角形.
试题解析:
(1)连接BC,如图所示:
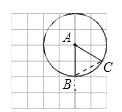
由网格可知点C在AB的中垂线上,
∴AC=BC,
∵AB=AC,∴AB=BC=AC,即△ABC是等边三角形.
∴∠ABC=60°;
(2)如图所示:
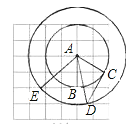
∵CD切⊙A于点C,
∴∠ACD=90°∠ABE=∠ACD=90°,
在Rt△AEB与Rt△ADC中,
∵AB=AC,AE=AD.
∴Rt△AEB≌Rt△ADC(HL);
(3)△AEB可以看作是由△ADC绕点A顺时针旋转60°得到的.△AED是等边三角形;
(4)①在直线a上任取一点,记为点A′,作A′M′⊥b,垂足为点M′;②作线段A′M′的垂直平分线,此直线记为直线d;③以点A′为圆心,A′M′长为半径画圆,与直线d交于点N′;④过点N′作N′C′⊥A′N′交直线c于点C′,连接A′C′;⑤以点A′为圆心,A′C′长为半径画圆,此圆交直线b于点B′;⑥连接A′B′、B′C′,则△A′B′C′为所求等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,小明的父亲在相距![]() 米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是
米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是![]() 米,绳子自然下垂呈抛物线状,身高
米,绳子自然下垂呈抛物线状,身高![]() 米的小明距较近的那棵树
米的小明距较近的那棵树![]() 米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加。
(1)根据图中所提供的信息,回答下列问题:2008年绿地面积为 公顷。
在2006、2007、2008年这三年中,绿地面积增加最多的是 年。
(2)为了满足城市发展的需要,计划到2010年使绿地总面积达到72.6公顷,试求这两年(2008——2010)绿地面积的年平均增长率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场,草莓的批发价格是每箱![]() 元,苹果的批发价格是每箱
元,苹果的批发价格是每箱![]() 元.
元.
(1)若李心批发草莓,苹果共![]() 箱,刚好花费
箱,刚好花费![]() 元,则他购买草莓、苹果各多少箱.
元,则他购买草莓、苹果各多少箱.
(2)李心有甲,乙两个店铺,每个店铺在同一时间段内都能售出草莓,苹果两种水果合计![]() 箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为
箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为![]() 元和
元和![]() 元,乙店铺获毛利润分别为
元,乙店铺获毛利润分别为![]() 元和
元和![]() 元.现在,李心要将批发购进的
元.现在,李心要将批发购进的![]() 箱草莓,
箱草莓,![]() 箱苹果分配给每个店铺各
箱苹果分配给每个店铺各![]() 箱.设分配给甲店草莓
箱.设分配给甲店草莓![]() 箱.
箱.
①根据信息填表:
草莓数量(箱) | 苹果数量(箱) | 合计(箱) | |
甲店 |
|
| |
乙店 |
|
②设李心获取的总毛利润为![]() 元,
元,
(1)求![]() 与
与![]() 的函数关系式:
的函数关系式:
(2)若在保证乙店铺获得毛利润不少于![]() 元的前提下,应怎样分配水果,使总毛利润
元的前提下,应怎样分配水果,使总毛利润![]() 最大,最大的总毛利润是多少元.
最大,最大的总毛利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.
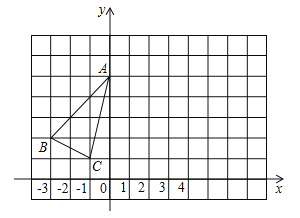
(1)画出△ABC关于y轴对称的△AB1C1, 并写出B1的坐标;
(2)将△ABC向右平移8个单位, 画出平移后的△A2B2C2, 写出B2的坐标;
(3)认真观察所作的图形, △AB1C1与△A2B2C2有怎样的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.
(1)若△CDE的周长为4,求AB的长;
(2)若∠ACB=100°,求∠DCE的度数;
(3)若∠ACB=a(90°<a<180°),则∠DCE=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:

![]() 求出样本容量,并补全直方图;
求出样本容量,并补全直方图;
![]() 该年级共有学生
该年级共有学生![]() 人,请估计全年级在这天里发言次数不少于
人,请估计全年级在这天里发言次数不少于![]() 次的人数;
次的人数;
![]() 已知
已知![]() 组发言的学生中恰有
组发言的学生中恰有![]() 位女生,
位女生,![]() 组发言的学生中恰有
组发言的学生中恰有![]() 位男生,现从
位男生,现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com