练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某城区近几年通过拆迁旧房，植草，栽树，修建公园等措施，使城区绿地面积不断增加。

    （1）根据图中所提供的信息，回答下列问题：2008年绿地面积为 公顷。

    在2006、2007、2008年这三年中，绿地面积增加最多的是 年。

    （2）为了满足城市发展的需要，计划到2010年使绿地总面积达到72.6公顷，试求这两年（2008——2010）绿地面积的年平均增长率。

    【答案】（1）60；2007．（2）10%.

    【解析】

    （1）通过折线统计图上的数据就能得到答案；

    （2）从图上可看出2008年的绿地面积为60公顷；题目给出2010年为72.6公顷，根据条件可列出方程求解．

    （1）从图上可看出2008年对应的绿地面积数据是60；2006年增加面积是51-48=3，2007年为56-51=5，2008年为60-56=4，故增加最多的是2007年．

    故答案为60；2007．

    （2）设这两年（2008-2010）绿地面积的年平均增长率为x．

    60（1+x）2=72.6，

    x=0.1或x=-2.1（舍去）．

    答：绿地面积的年平均增长率为10%．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某种流感病毒，有一人患了这种流感，在每轮传染中一人将平均传给x人．

    （1）求第一轮后患病的人数；（用含x的代数式表示）

    （2）在进入第二轮传染之前，有两位患者被及时隔离并治愈，问第二轮传染后总共是否会有21人患病的情况发生，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，面积为4的正方形OABC的顶点O与坐标原点重合，边OA、OC分别在x轴、y轴的正半轴上，点B、P都在函数y=（x＞0）的图象上，过动点P分别作轴x、y轴的平行线，交y轴、x轴于点D、E．设矩形PDOE与正方形OABC重叠部分图形的面积为S，点P的横坐标为m．

    （1）求k的值；

    （2）用含m的代数式表示CD的长；

    （3）求S与m之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

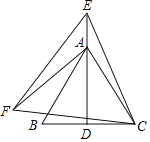
    【题目】如图，D为等边△ABC中边BC的中点，在边DA的延长线上取一点E，以CE为边、在CE的左下方作等边△CEF，连结AF．若AB＝4，AF＝，则CF的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABE与△CDE都是等腰直角三角形，∠AEB＝∠DEC＝90°，连接AD，AC，BC，BD，若AD＝AC＝AB，则下列结论：①AE垂直平分CD，②AC平分∠BAD，③△ABD是等边三角形，④∠BCD的度数为150°，其中正确的个数是（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图中的图象（折线ABCDE）描述了一汽车在某一直道上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系．根据图中提供的信息，给出下列说法：

    ①汽车共行驶了120千米；

    ②汽车在行驶途中停留了0.5小时；

    ③汽车在整个行驶过程中的平均速度为千米/时；

    ④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．

    其中正确的说法有（　　）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形网格中以点A为圆心，AB为半径作圆A交网格于点C（如图（1）），过点C作圆的切线交网格于点D，以点A为圆心，AD为半径作圆交网格于点E（如图（2））．

    问题：

    （1）求∠ABC的度数；

    （2）求证：△AEB≌△ADC；

    （3）△AEB可以看作是由△ADC经过怎样的变换得到的？并判断△AED的形状（不用说明理由）．

    （4）如图（3），已知直线a，b，c，且a∥b，b∥c，在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′，B′，C′，分别在直线a，b，c上．要求写出简要的画图过程，不需要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

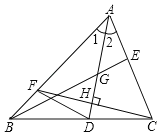
    【题目】如图所示，在△ABC中，AD是∠BAC的平分线，G是AD上一点，且AG＝DG，连接BG并延长BG交AC于E，又过C作AD的垂线交AD于H，交AB为F，则下列说法正确的是_____（填序号）．

    ①D是BC的中点；②∠CDA＞∠2；③BE是△ABC的边AC上的中线；

    ④CH为△ACD的边AD上的高；⑤△AFC为等腰三角形；

    ⑥连接DF，若CF＝6，AD＝8，则四边形ACDF的面积为24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线x=-4与x轴交于点E，一开口向上的抛物线过原点交线段OE于点A，交直线x=-4于点B，过B且平行于x轴的直线与抛物线交于点C，直线OC交直线AB于D，且AD：BD=1：3．

    （1）求点A的坐标；

    （2）若△OBC是等腰三角形，求此抛物线的函数关系式．

    查看答案和解析>>

    同步练习册答案