
【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=![]() (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

【答案】(1)k=4;(2)当0<m≤2时,CD=![]() ﹣2;当m>2时,CD=2﹣
﹣2;当m>2时,CD=2﹣![]() ;(3)当0<m≤2时,S=2m
;(3)当0<m≤2时,S=2m
当m>2时,S=![]() ;
;
【解析】
(1)利用正方形的性质的OA=AB=2,则B点则坐标可以求出,将B点坐标代入反比例函数的解析式,即可求出k的值.
(2)分类:P(m,n)在![]() 上,得到mn=4,分以下几类:
上,得到mn=4,分以下几类:
当x>2时,S=AE·PE=![]() ,即可求出n的值;
,即可求出n的值;
当0<x≤2时,S=P'F'·F'C=![]() ,即可求出m的值,
,即可求出m的值,
即可确定P的坐标.
(3)由(2)可以求出x>2与0<x≤2时所对应S的表达式.
(1)∵正方形OABC的面积4,
∴BA=BC=OA=OC=2.
∴点 B(2,2),
∵点B、P都在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=2×2=4,
∴解析式y=![]() ,
,
(2)∵点P在y=![]() 的图象上,且横坐标为m,
的图象上,且横坐标为m,
∴![]() ,
,
当0<m≤2时,CD=![]() ﹣2,
﹣2,
当m>2时,CD=2﹣![]() ,
,
(3)当0<m≤2时,S=2m,
当m>2时,S=2×![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,小明的父亲在相距![]() 米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是
米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是![]() 米,绳子自然下垂呈抛物线状,身高
米,绳子自然下垂呈抛物线状,身高![]() 米的小明距较近的那棵树
米的小明距较近的那棵树![]() 米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=![]() (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )

A. 1 B. ![]() C. 2
C. 2![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
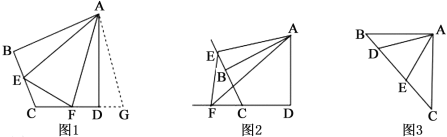
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线,易证△AFG≌△AFE,故EF,BE,DF之间的数量关系为__;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() 可以转化为指数式
可以转化为指数式![]() .
.
根据以上材料,解决下列问题:
(1)计算:![]() ,
,![]() ,
,![]() ;
;
(2)观察(1)中的三个数,猜测:![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ),并加以证明这个结论;
),并加以证明这个结论;
(3)已知:![]() ,求
,求![]() 和
和![]() 的值(
的值(![]() 且
且![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加。
(1)根据图中所提供的信息,回答下列问题:2008年绿地面积为 公顷。
在2006、2007、2008年这三年中,绿地面积增加最多的是 年。
(2)为了满足城市发展的需要,计划到2010年使绿地总面积达到72.6公顷,试求这两年(2008——2010)绿地面积的年平均增长率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com