
分析 (1)直接利用已知例题进行配方化简即可;
(2)①首先提取公因式$\sqrt{3}$,再进行配方化简即可;
②首先提取公因式$\sqrt{2}$,再进行配方化简即可;
(3)利用根号下部分乘2进而配方化简即可.
解答 解:(1)$\sqrt{5-2\sqrt{6}}$=$\sqrt{(\sqrt{3}-\sqrt{2})^{2}}$=$\sqrt{3}$-$\sqrt{2}$;
$\sqrt{12+2\sqrt{35}}$=$\sqrt{(\sqrt{7}+\sqrt{5})^{2}}$=$\sqrt{7}$+$\sqrt{5}$;
故答案为:$\sqrt{3}$-$\sqrt{2}$;$\sqrt{7}$+$\sqrt{5}$;
(2)①$\sqrt{9+6\sqrt{2}}$=$\sqrt{3}$•$\sqrt{3+2\sqrt{2}}$=$\sqrt{3}$($\sqrt{2}$+1)=$\sqrt{6}$+$\sqrt{3}$;
②$\sqrt{16-4\sqrt{15}}$
=$\sqrt{2}$•$\sqrt{8-2\sqrt{15}}$
=$\sqrt{2}$($\sqrt{5}$-$\sqrt{3}$)
=$\sqrt{10}$-$\sqrt{6}$;
(3)$\sqrt{3-\sqrt{5}}+\sqrt{2+\sqrt{3}}$
=$\frac{\sqrt{6-2\sqrt{5}}}{\sqrt{2}}$+$\frac{\sqrt{4+2\sqrt{3}}}{\sqrt{2}}$
=$\frac{\sqrt{5}-1+\sqrt{3}+1}{\sqrt{2}}$
=$\frac{\sqrt{10}+\sqrt{6}}{2}$.
点评 此题主要考查了二次根式的化简求值,正确应用完全平方公式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
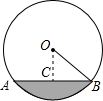 一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )| A. | 4 | B. | 5 | C. | 6$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某轮船在O处,测得灯塔A在它北偏东40°的方向上,渔船B在它的东南方向上,则∠AOB的度数是( )
如图,某轮船在O处,测得灯塔A在它北偏东40°的方向上,渔船B在它的东南方向上,则∠AOB的度数是( )| A. | 85° | B. | 90° | C. | 95° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,OC是∠AOB的平分线.
已知:如图,OC是∠AOB的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平行四边形ABCD中,E、F分别为AB、AD上的点,且BE=2AE,AF=3DF,连结EF、AC,交于点G,则$\frac{AG}{CG}$的值为$\frac{3}{10}$.
如图,平行四边形ABCD中,E、F分别为AB、AD上的点,且BE=2AE,AF=3DF,连结EF、AC,交于点G,则$\frac{AG}{CG}$的值为$\frac{3}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com