
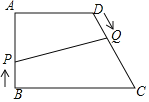
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=AD=8cm,CD=10cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为lcm/s.连接PQ,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,PQ∥AD?
(2)设四边形APQD的面积为y(cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APQO:S四边形BCQP=17:27?若存在,求出t的值,并求此时PQ的长;若不存在,请说明理由.
【答案】(1)当t为![]() s时,PQ∥AD;(2)y与t的函数关系式是y=
s时,PQ∥AD;(2)y与t的函数关系式是y=![]() ;(3)t的值为2s或
;(3)t的值为2s或![]() s,此时PQ的长为
s,此时PQ的长为![]() cm,见解析.
cm,见解析.
【解析】
(1)根据平行线分线段成比例的性质解答即可;
(2)过点D作DE⊥BC于点E,过点Q作QF⊥AD交AD的延长线于F,根据矩形的性质和三角函数解答即可;
(3)过点Q作QH⊥AB于点H,根据四边形面积公式进行解答即可.
解:(1)∵PQ∥AD,AD∥BC
∴![]() ,
,
即![]()
解得,![]()
答:当t为![]() s时,PQ∥AD.
s时,PQ∥AD.
(2)过点D作DE⊥BC于点E,过点Q作QF⊥AD交AD的延长线于F
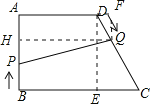
∴∠DEC=∠QFD=90°
∵AD∥BC,∠A=90°
∴∠ABC=180°-∠A=90°
∴四边形ABND是矩形
∴AB=DE,BE=AD
在Rt△DEC中,![]() ,
,
∵∠C=∠QDF
∴在Rt△DFQ和Rt△DEC中,
sin∠QDF=![]() ,即
,即![]()
∴![]()
cos∠QDF=![]() ,即
,即![]()
∴![]()
∵在四边形ABCD中,∠A=90°,AB=AD
∴∠ABD=∠ADB=45°
∴y=S四边形APQD=S四边形APQF-S△DQF
=![]()
=![]()
=![]()
答:y与t的函数关系式是y=![]() .
.
(3)若S四边形APQD:S四边形BCQP=17:27,则y=![]() S四边形ABCD
S四边形ABCD
∵S四边形ABCD=![]()
∴![]() =34
=34
解得t1=2,![]()
∴t的值为2s或![]() s.
s.
过点Q作QH⊥AB于点H,
∴PH=![]()
QH=AF=![]()
∴PQ=![]()
当t=2时,PQ=![]()
当t=![]() 时,PQ=
时,PQ=![]()
∴此时PQ的长为![]() cm.
cm.


科目:初中数学 来源: 题型:
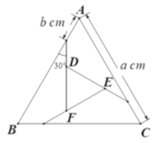
【题目】如图,把边长为![]() cm的等边
cm的等边![]() 剪成四部分,从三角形三个顶点往下bcm处,呈30°角下剪刀,使中间部分形成一个小的等边
剪成四部分,从三角形三个顶点往下bcm处,呈30°角下剪刀,使中间部分形成一个小的等边![]() .若
.若![]() 的面积是
的面积是![]() 的
的![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
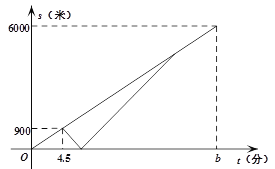
【题目】周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
(1)求a、b的值.
(2)求甲追上乙时,距学校的路程.
(3)当两人相距500米时,直接写出t的值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
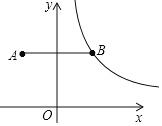
【题目】在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=![]() (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
(1)求k的值;
(2)若△ABP的面积等于2,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,动点
两点,动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,以
方向运动,以![]() 为边作矩形
为边作矩形![]() (点
(点![]() 在
在![]() 轴上),设运动的时间为
轴上),设运动的时间为![]() 秒.
秒.
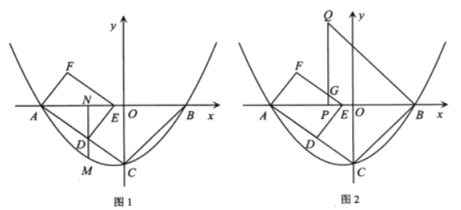
(1)求抛物线![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)如图,动点![]() 同时从点
同时从点![]() 出发,以每秒3个单位长度的速度沿
出发,以每秒3个单位长度的速度沿![]() 方向运动,以
方向运动,以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() .给出如下定义:在四边形
.给出如下定义:在四边形![]() 中,
中,![]() ,
,![]() 且
且![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.当矩形
,我们把这种两组邻边分别相等的四边形叫做“筝形”.当矩形![]() 和等腰三角形
和等腰三角形![]() 重叠的四边形是“筝形”时,求“筝形”的面积.
重叠的四边形是“筝形”时,求“筝形”的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
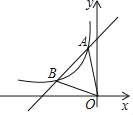
【题目】如图,曲线l是由函数y=![]() 在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A (m,6),B (﹣6,n),则△OAB的面积为_____.
在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A (m,6),B (﹣6,n),则△OAB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
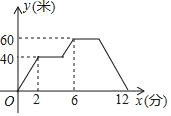
【题目】小明在练习操控航拍无人机,该型号无人机在上升和下落时的速度相同,设无人机的飞行高度为y(米),小明操控无人飞机的时间为x(分),y与x之间的函数图象如图所示.
(1)无人机上升的速度为 米/分,无人机在40米的高度上飞行了 分.
(2)求无人机下落过程中,y与x之间的函数关系式.
(3)求无人机距地面的高度为50米时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com