
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.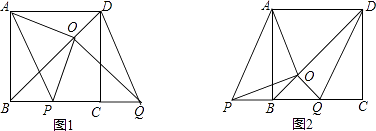
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB , BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
【答案】
(1)解:四边形APQD为平行四边形;
(2)解:OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
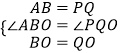
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(3)解:如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
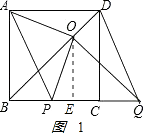
则BQ=x+2,OE= ![]() ,
,
∴y= ![]() ×
× ![]() x,即y=
x,即y= ![]() (x+1)2﹣
(x+1)2﹣ ![]() ,
,
又∵0≤x≤2,
∴当x=2时,y有最大值为2;
②如图2,当P点在B点左侧时,
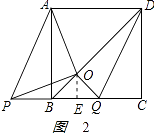
则BQ=2﹣x,OE= ![]() ,
,
∴y= ![]() ×
× ![]() x,即y=﹣
x,即y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
又∵0≤x≤2,
∴当x=1时,y有最大值为 ![]() ;
;
综上所述,∴当x=2时,y有最大值为2;
【解析】(1)根据平移的性质,可得PQ∥AD且PQ=AD,然后根据一组对边平行且相等的四边形是平行四边形进行证明即可;
(2)先证明△BOQ为等腰直角三角形,从而可得到∠OQP=∠ABO,由平移的性质和正方形的性质可得到PQ=AB,然后依据SAS可证明△AOB≌△POQ,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式可得到y与x的二次函数关系式,最后,根据二次函数的性质求解即可.


科目:初中数学 来源: 题型:
【题目】阅读第(1)题解答过程填理由,并解答第(2)题
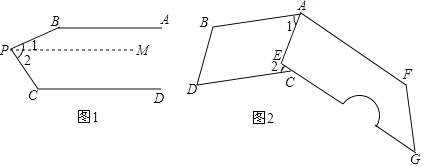
(1)已知:如图1,AB∥CD,P为AB,CD之间一点,求∠B+∠C+∠BPC的大小.
解:过点P作PM∥AB
∵AB∥CD(已知)
∴PM∥CD ,
∴∠B+∠1=180°, .
∴∠C+∠2=180°
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
(2)我们生活中经常接触小刀,如图2小刀刀柄外形是一个直角梯形挖去一个小半圈,其中AF∥EG,∠AEG=90°,刀片上、下是平行的(AB∥CD),转动刀片时会形成∠1和∠2,那么∠1+∠2的大小是否会随刀片的转动面改变,如不改变,求出其大小;如改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,有下列说法:①点
,有下列说法:①点![]() 与点
与点![]() 的距离是线段
的距离是线段![]() 的长;②点
的长;②点![]() 到直线
到直线![]() 的距离是线段
的距离是线段![]() 的长;③线段
的长;③线段![]() 是
是![]() 边
边![]() 上的高;④线段
上的高;④线段![]() 是
是![]() 边
边![]() 上的高.
上的高.
上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王警官骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,-8,+7,-15,+6,-16,+4,-2,+9.
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+ ![]() )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.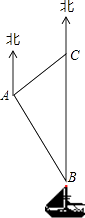
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①倒数等于本身的数是±1;②互为相反数的两个非零数的商为﹣1;③如果两个数的绝对值相等,那么这两个数相等;④有理数可以分为正有理数和负有理数;⑤单项式﹣![]() 的系数是﹣
的系数是﹣![]() ,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
A. 2 个B. 3 个C. 4 个D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
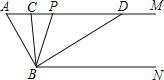
(1)求∠CBD的度数;
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com