
����Ŀ��ij���������ɼ�������������ļ۸�Ϊ![]() Ԫʱ��ÿ����ס�Ĺ�����Ϊ
Ԫʱ��ÿ����ס�Ĺ�����Ϊ![]() �䣬���г�����������ñ���ÿ������ļ۸���
�䣬���г�����������ñ���ÿ������ļ۸���![]() Ԫ֮�䣨��
Ԫ֮�䣨��![]() Ԫ��
Ԫ��![]() Ԫ������ʱ��ÿ����ס�ķ�����
Ԫ������ʱ��ÿ����ס�ķ�����![]() ���䣩��ÿ������ļ۸�
���䣩��ÿ������ļ۸�![]() ��Ԫ�����������±���
��Ԫ�����������±���
| ���� | 190 | 200 | 210 | 220 | ���� |
| ���� | 65 | 60 | 55 | 50 | ���� |
��1��������������������ϵ�������Ӧ�ĵ㣬������ͼ��
��2�����루1���е�ͼ����ʲô������ͼ����![]() ����
����![]() �ĺ�������ʽ����д���Ա���
�ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����ͷ�����Ӫҵ��ΪW (Ԫ)�����������������أ��ʱ��ݱ����ļ۸�Ϊ����Ԫʱ���ͷ�����Ӫҵ��������Ϊ����Ԫ��
���𰸡���1������������2��һ�κ�����y=![]() x+160��170��x��240������3�����ݱ����ļ۸�Ϊ170Ԫʱ���ͷ�����Ӫҵ�����Ϊ12750Ԫ.
x+160��170��x��240������3�����ݱ����ļ۸�Ϊ170Ԫʱ���ͷ�����Ӫҵ�����Ϊ12750Ԫ.
��������
��1��������������ݣ���㡢�����ɵã�
��2������ͼ��ɲ���Ϊһ�κ����������ô���ϵ�������ɵã�
��3����Ӫҵ��=��ס�������������۵ó���������ʽ�������ö��κ������������ɵã�
�⣺��1����ͼ��ʾ��
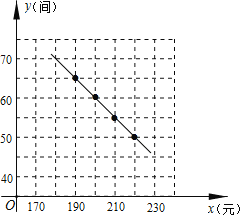
��2����ͼ��ɲ��룺��1���е�ͼ����һ�κ���ͼ��
��y=kx+b��
����200��60������220��50�����룬
�ã�![]() ��
��
��ã�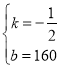 ��
��
��y=![]() x+160��170��x��240����
x+160��170��x��240����
��3��W=xy=x��![]() x+160��=
x+160��=![]() x2+160x��
x2+160x��
��Գ���Ϊֱ��x=![]() =160��
=160��
��a=![]() ��0��
��0��
����170��x��240��Χ�ڣ�w��x���������С��
�൱x=170ʱ��w�����ֵ�����ֵΪ12750Ԫ��
����ݱ����ļ۸�Ϊ170Ԫʱ���ͷ�����Ӫҵ�����Ϊ12750Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������A=30����BDΪ��ABC�Ľ�ƽ���ߣ���AC= 12 ,������ABD��AB���ϵĸ�Ϊ�� ��
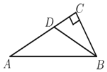
A.3B.4C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
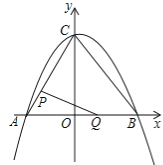
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У����κ���y��![]() x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
��1����գ�b�� ��c�� ��
��2���ڵ�P��Q�˶������У���APQ������ֱ������������˵�����ɣ�
��3����M���������ϣ��ҡ�AOM��������AOC�������ȣ������M�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������Ҫ�øֹ����������������Ҫ��������Ҫ��Ϊ 0.8m��2.5m �Ҵ�ϸ��ͬ�ĸֱֹܷ�Ϊ 100 ����32 ������Ҫ����Щ���ϲ����Ǻ��Ӷ��ɵģ��ֲָ��г������ֹ��ĸֹ�ÿ��Ϊ 6m��
��1������һ�� 6m ����Բ�ֹ�����Щ�ü������أ�����д�¿գ��������ϣ���
�����٣���ֻ�ü���Ϊ 0.8m ������ʱ�����ɼ� ����
�����ڣ����ȼ��� 1 �� 2.5m ������ʱ�����²�������ܼ� 0.8m �������� ����
�����ۣ����ȼ��� 2 �� 2.5m ������ʱ�����²�������ܼ� 0.8m �������� ����
��2���ֱ��ã�1���еķ����ںͷ����۸��ü����ٸ� 6m ���ĸֹܣ����ܸպõõ�����Ҫ����Ӧ�����IJ��ϣ�
��3����̽��������2���з����⣬�ڣ�1���л��������ַ������ϣ�����Ҫ 6m ���ĸֹ��루2�� �и�����ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ƽ��ֱ������ϵ��A��5��0����BΪy��������һ�㣬�Ե�BΪֱ�Ƕ���������Rt��ABC����A��B��C��˳ʱ�뷽�����У�����̽����C�Ƿ���һȷ����ֱ���ϣ�
��2����ƽ��ֱ������ϵ�У�A����1��0����B��4��2m��������AB����AB�Ƶ�B��ʱ����ת90�㵽CB����̽����C�Ƿ���һȷ����ֱ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
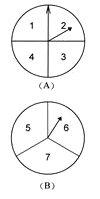
����Ŀ��������������ת����Ϸʱ����ת��A��B�ֱ�ֳ�4�ȷݡ�3�ȷݣ�����ÿһ���ڱ������֣���ͼ��ʾ����Ϸ�涨��ת������ת��ֹͣ��ָ����ָ����������֮��Ϊ����ʱ����ʤ��Ϊż��ʱ���һ�ʤ��
��1�����б���������״ͼ�����ʤ�ĸ��ʣ�
��2������Ϊ�����Ϸ�����˫����ƽ�����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90�㣬AC=BC=3cm.����P�ӵ�A��������![]() cm/s���ٶ���AB�����˶�����B.����Qͬʱ�ӵ�A��������1cm/s���ٶ�������AC
cm/s���ٶ���AB�����˶�����B.����Qͬʱ�ӵ�A��������1cm/s���ٶ�������AC![]() CB�����˶�����B.����APQ�����Ϊy��cm2��.�˶�ʱ��Ϊx��s����������ͼ���ܷ�ӳy��x֮���ϵ���� �� ��
CB�����˶�����B.����APQ�����Ϊy��cm2��.�˶�ʱ��Ϊx��s����������ͼ���ܷ�ӳy��x֮���ϵ���� �� ��

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
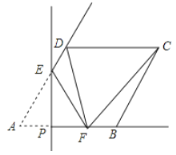
����Ŀ����ͼ���ڱ߳�Ϊ2������![]() �У�
��![]() ����
����![]() ����
Ϊ����![]() ��һ�����㣬����
��һ�����㣬����![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() �۵�����
�۵�����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ������
������![]() ��
��![]() ����
����![]() Ϊֱ��������ʱ��
Ϊֱ��������ʱ��![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ���㣬�����ߵĶ����Ϊ
���㣬�����ߵĶ����Ϊ![]() ����Գ�����
����Գ�����![]() ��Ľ����Ϊ
��Ľ����Ϊ![]() ��
��
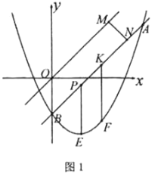
��1����ͼ1�����߶�![]() ������������
������������![]() ��
��![]() ����
����![]() ����
����![]() �ᣬ�ֱ��������ڵ�
�ᣬ�ֱ��������ڵ�![]() ��
��![]() ������
������![]() ����һ��ֱ��
����һ��ֱ��![]() ����
����![]() ȡ�����ֵʱ����һ����
ȡ�����ֵʱ����һ����![]() ��
��![]() ������ij��·����1����λÿ����ٶ����˶���ֱ��
������ij��·����1����λÿ����ٶ����˶���ֱ��![]() �ϵĵ�
�ϵĵ�![]() �������ش�ֱ��
�������ش�ֱ��![]() �ķ�����1����λÿ����ٶȴӵ�
�ķ�����1����λÿ����ٶȴӵ�![]() �˶���
�˶���![]() ��
��![]() �㴦�������
�㴦�������![]() ����λÿ����ٶȴӵ�
����λÿ����ٶȴӵ�![]() �ص���
�ص���![]() ���˶�ֹͣ�����������������
���˶�ֹͣ�����������������![]() �����꼰����
�����꼰����![]() �˶���ʱ�����Сֵ��
�˶���ʱ�����Сֵ��
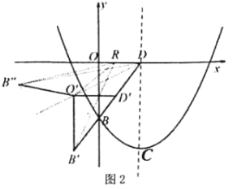
��2����ͼ2������![]() ����
����![]() ������
������![]() ƽ�Ƶ�
ƽ�Ƶ�![]() ����
����![]() ǡ�����ڡ�BDO�Ľ�ƽ������ʱ����
ǡ�����ڡ�BDO�Ľ�ƽ������ʱ����![]() ����ȡһ��
����ȡһ��![]() ���ٽ�
���ٽ�![]() ��
��![]() ���۵�
���۵�![]() ������
������![]() ��
��![]() ����
����![]() Ϊ����������ʱ�����
Ϊ����������ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com